What is not a polygon: General Data Protection Regulation(GDPR) Guidelines BYJU’S

Classifying Polygons

Closed shapes or figures in a plane with three or more sides are called polygons. Alternatively, a polygon can be defined as a closed planar figure that is the union of a finite number of line segments. In this definition, you consider closed as an undefined term. The term polygon is derived from a Greek word meaning “many‐angled.”

Polygons first fit into two general categories— convex and not convex (sometimes called concave). Figure 1 shows some convex polygons, some non‐convex polygons, and some figures that are not even classified as polygons.

Figure 1 Which are polygons? Which of the polygons are convex?

Identifying the parts of a polygon

The endpoints of the sides of polygons are called vertices. When naming a polygon, its vertices are named in consecutive order either clockwise or counterclockwise.

Consecutive sides are two sides that have an endpoint in common. The four‐sided polygon in Figure could have been named ABCD, BCDA, or ADCB, for example. It does not matter with which letter you begin as long as the vertices are named consecutively. Sides AB and BC are examples of consecutive sides.

Figure 2 There are four pairs of consecutive sides in this polygon.

A diagonal of a polygon is any segment that joins two nonconsecutive vertices. Figure 3 shows five‐sided polygon QRSTU. Segments QS , SU , UR , RT and QT are the diagonals in this polygon.

Figure 3 Diagonals of a polygon.

Number of sides

Polygons are also classified by how many sides (or angles) they have. The following lists the different types of polygons and the number of sides that they have:

• A triangle is a three‐sided polygon.

• A quadrilateral is a four‐sided polygon.

• A pentagon is a five‐sided polygon.

• A hexagon is a six‐sided polygon.

• A septagon or heptagon is a seven‐sided polygon.

• An octagon is an eight‐sided polygon.

• A nonagon is a nine‐sided polygon.

• A decagon is a ten‐sided polygon.

An earlier chapter showed that an equilateral triangle is automatically equiangular and that an equiangular triangle is automatically equilateral. This does not hold true for polygons in general, however. Figure shows examples of quadrilaterals that are equiangular but not equilateral, equilateral but not equiangular, and equiangular and equilateral.

Figure 4 An equiangular quadrilateral does not have to be equilateral, and an equilateral quadrilateral does not have to be equiangular.

Regular polygons

When a polygon is both equilateral and equiangular, it is referred to as a regular polygon. For a polygon to be regular, it must also be convex. Figure shows examples of regular polygons.

Figure 5 Regular polygons.

What Are Polygons (Video)

Hi and welcome to this video about polygons! In this video we will explore four things:

1. What polygons are
2. The different parts of a polygon
3. Ways to classify polygons
4. How to determine the number of diagonals in a polygon

The term polygon is derived from the Greek words polys meaning “many” and gonia meaning “angle”. So, polygons have many angles.

First let’s explore how polygons are constructed.

Consider the geometric point, represented by a dot:

The point is 0-dimensional – it has no length, width, height, nothing.

Now, let’s consider two connected points:

This is called a line, or a line segment. A line segment is 1-dimensional. It has length, but no width or height.

When multiple line segments are connected end-to-end, polygons such as this, can be formed:

Polygons are 2-dimensional. They have no thickness, like this.

In order to be a polygon, the shape must be closed. In other words, every endpoint must be connected to another endpoint. This figure is comprised of connected segments, but the result is not a polygon.

This shape is closed, but not made up of connected segments, so it is also not a polygon:

A polygon is defined as a 2-dimensional closed shape composed of line segments.
The sides of polygons are called edges and the angles created where the edges intersect are called vertices. Polygons also have as many edges as vertices:

Polygons are named by the number of edges they have. This polygon has 3 edges, 3 vertices and is called a triangle. The triangle has the smallest number of edges and vertices of any polygon – it is impossible to create a 2-sided polygon.

Some common polygons are quadrilaterals (which have 4 sides), pentagons (which have 5 sides), hexagons (6 sides), heptagons (7 sides), octagons (8 sides), nonagons (9 sides), decagons (10 sides) and dodecagons (which have 12 sides).

Though polygons with any number of edges have names, the general n-gon is typically used for all other polygons, where n represents the number of sides. For instance, a 30-sided polygon is called a triacontagon, but it’s often simply called a 30-gon.

Polygons can be regular or irregular. Regular polygons have congruent edges and congruent vertices. For example:

This is a regular quadrilateral. The edges are the same length and the vertices have the same measure.

This is an irregular quadrilateral. The vertices have the same measure, but the edges have different lengths.

This is an irregular quadrilateral. The edges are the same length, but the vertices have different measures.

This is an irregular quadrilateral. Neither the edges nor the vertices have the same measure.

Polygons can also be convex or concave. When one or more vertices of a polygon measures more than 180 degrees, the result is a concave polygon. For example:

This is a convex hexagon. All of the vertices measure less than 180 degrees.

This is a Concave hexagon. One vertex measures more than 180°.

Now remember:

• Only polygons with 4 or more sides can be concave because it’s not possible for a triangle to contain an angle measuring more than 180°, which is a straight line.
• Concave polygons cannot be regular because all the vertices will never be the same measure.

Polygons also contain diagonals. Diagonals are line segments joining two vertices that are not next to each other.

As you can see here, this irregular convex pentagon has 5 diagonals.

This is an irregular concave pentagon.

It also has 5 diagonals, even though the concavity causes diagonals to lie outside the polygon.

Triangles do not have diagonals because there is no way to connect two vertices with segments that are not edges.

Now that you know the basics of polygons, let’s use the diagrams to figure out a formula for finding the number of diagonals in any polygon.

In this case, the number of diagonals connecting to each vertex is 2, which is 3 less than the number of vertices, 5: 2 diagonals connected to each vertex.

This is true of all diagonals of all polygons. A nonagon has \(9-3=6\) diagonals connecting to each vertex.

The number 3 is not arbitrary here – from any vertex, diagonals cannot connect to the vertex itself or to the vertices that they are “1 away” from, because it would be edges. That makes 3 vertices from every vertex that aren’t included. To generalize this, we’ll use \(n-3\), where n is the number of vertices of the polygon.

Now, each vertex has the same number of diagonals connecting to it, so in this case, we can see that the total number of diagonal connections to vertices is \(5(5-3)=10\).

In general, we can say the total number of diagonal connections is \(n(n-3)\).

When we figure out this total, though, we are counting each diagonal twice, because diagonals have 2 endpoints. In order to figure out the number of unique diagonals, we need to divide our total by 2. In our pentagon, this looks like:

\(\frac{5(5-3)}{2} = 5\) unique diagonals
(which corresponds to our diagram)

Therefore, for any sized polygon: Our equation can be written as this:

\(\frac{n(n-3)}{2}\)
 
Conceptually, this can be remembered as:

\(\frac{(\text{total number of vertices})(\text{number of diagonal connections at each vertex})}{(\text{number of endpoints of each diagonal})}\)
 
Using our formula, we can determine the number of unique diagonals in, for example, a 17-gon:

\(\frac{17(17-3)}{2} = 119\text{ unique diagonals}\)
 
We can also see algebraically that triangles have no diagonals:

\(\frac{3(3-3)}{2} = 0\)
 
We can also figure out how many edges or vertices a polygon has by the number of unique diagonals.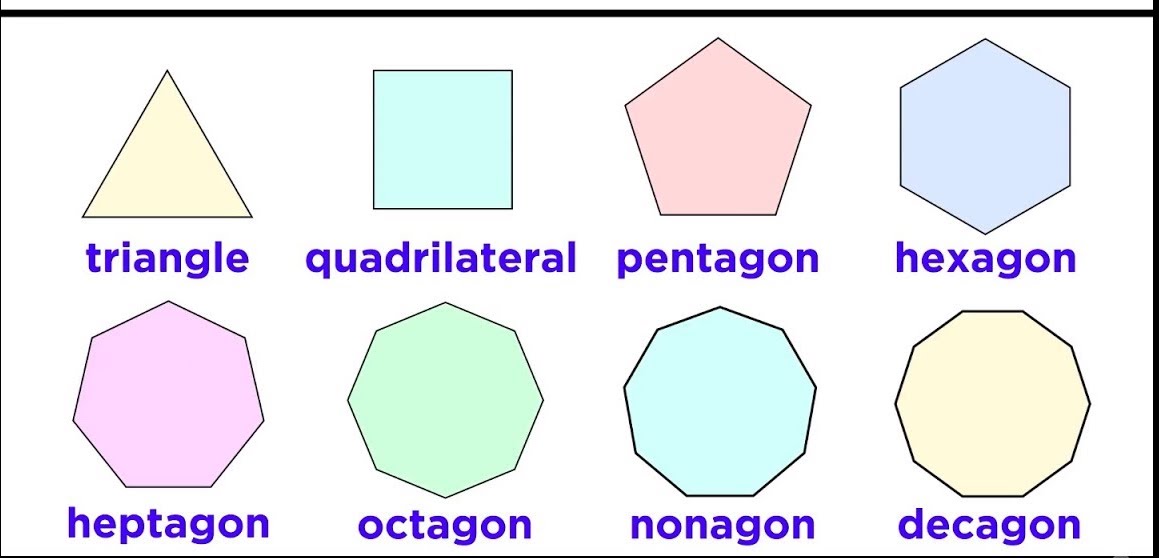 2 – 3n – 88 = 0\)

.

\((n + 8)(n-11) = 0\)

.

\(n = -8\text{ or }n = 11\)

.

Alright, so here we are at our answer, n (the number of edges the polygon has) is either equal to 11 or -8. Because what we want to do is we want to make sure that we end with a result of 0, which means that n, somewhere, has to be 11 or -8 in order to get us multiplying 0 by another answer, resulting in 0. Since n can’t be negative (cause we can’t have negative edges), it can’t be -8. So we know that our answer is 11. The number of edges is 11, making it an 11-gon.

Alright, excellent! I hope this video helped increase your knowledge of polygons and made some of their properties a little bit clearer! Thanks for watching, see you next time!

Question #1:

Choose which of the following is a polygon:

Show Answer

Answer:

The correct answer is A.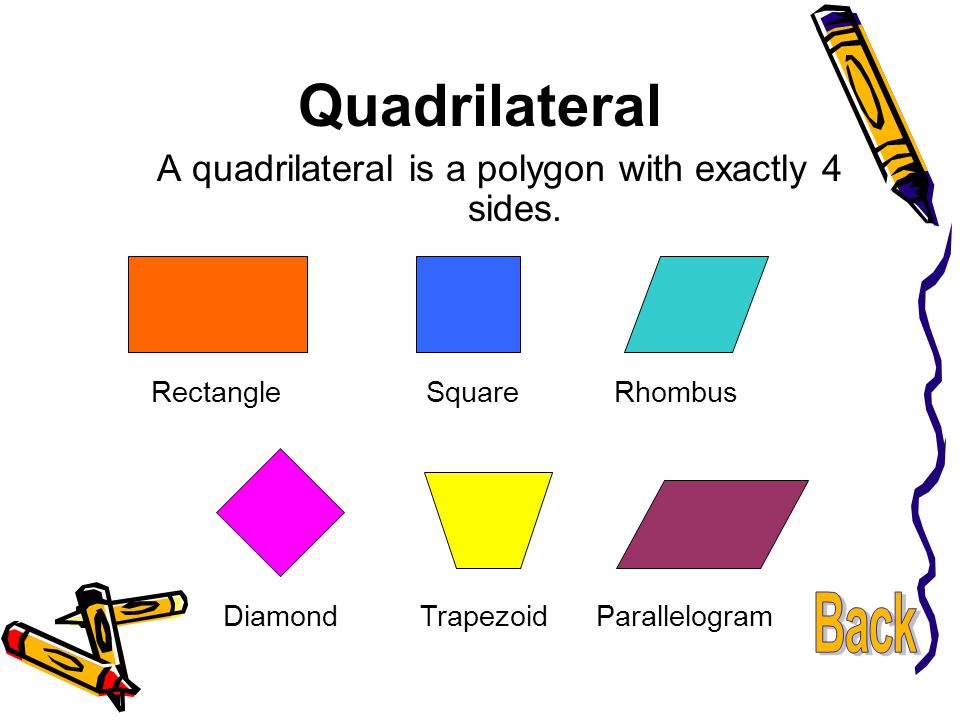 This shape is closed (every endpoint is connected to another endpoint), which is only possible when there are 3 or more “endpoints” or vertices– and there are just as many edges (sides) as there are vertices; making this a true polygon.

Let’s look into why answers B, C, and D are not polygons:

The circle is not a polygon because it is essentially just one continuous edge. There are no endpoints that we are connecting with individual line segments.

The spiral is not a polygon because it is not a closed shape. Additionally, there are only two endpoints/vertices.

Finally, the “No” symbol is clearly very similar to the circle. While it may be tempting to call it a polygon because there is a distinct edge connecting two vertices that runs through the middle of the shape, there are still only two vertices (and technically only one edge).

Hide Answer

Question #2:

Which of the following is an irregular polygon?

Show Answer

Answer:

The correct answer is B. While the equilateral triangle (Shape A), the square (Shape C), and the regular hexagon (Shape D) each have edges that are each the same length and same-degree angles at each vertex, the right triangle shown in Choice B has edges and angles that measure different lengths/degrees.

Hide Answer

Question #3:

Is this a concave or a convex polygon?

Concave

Convex

Show Answer

Answer:

The correct answer is A. This is a concave polygon, and we can see this in the top, right-hand portion of the shape:

This angle sitting inside of the polygon is larger than 180°. There’s a portion of the shape “caving in on itself.”

Hide Answer

Question #4:

How many unique diagonals does this polygon have?

48

40

28

20

Show Answer

Answer:

The correct answer is D. Since this shape is a relatively “simple” shape, we could feasibly count the diagonals by hand… but it would be far easier (and far more efficient) to use our given formula for determining the amount of unique diagonals in any polygon: \(\frac{n(n-3)}{2}\) (where n represents the amount of vertices [or edges] that that polygon has).

This octagon has 8 vertices, so we find that \(\frac{8(8-3)}{2}=20\).

Hide Answer

Question #5:

Given that some n-gon has 77 unique diagonals, find the value of n.

11

10

14

7

Show Answer

Answer:

The correct answer is C. This time, we must “work backwards” with our \(\frac{n(n-3)}{2}\) formula. We set our equation up like this:
\(\frac{n(n-3)}{2}=77\)
and our goal is to solve for n.
\(\frac{n(n-3)}{2}=77\)
\(n(n-3)=154\)
\(n^2-3n=154\)
\(n^2-3n-154=0\)

At this point, we’ll need to employ the quadratic formula to find the two possible solutions…
\(n=\frac{-(-3)\pm\sqrt{(-3)^2-4\times(1)\times(154)}}{2\times1}\)
\(n=\frac{3\pm\sqrt{9+(4\times154)}}{2}\)
\(n=\frac{3±\sqrt{9+616}}{2}\)
\(n=\frac{3±\sqrt{625}}{2}\)
\(n=\frac{3±25}{2}\)
\(n=14\) or \(n=-11\)

Out of these two possible solutions for n, only one of them makes sense for us! The value of n must be \(n=14\) because we cannot have a negative number of edges or vertices in a polygon.

Hide Answer

Polygon

Definition 1. A polygon is a closed broken line.

The union of a polygon and the part of the plane bounded by it is also called a polygon. Therefore, we present another definition of a polygon:

Definition 2. A polygon is a geometric figure that is part of a plane bounded by a closed polyline.

The vertices of the polyline are called vertices of the polygon. The links of the broken line are called sides polygon.

Any polygon divides the plane into two parts, one of which is called the inner area of ​​the polygon, and the other the outer area of ​​the polygon.

Types of polygons

A polygon with three vertices is called a triangle, with four vertices is called a quadrangle, with five vertices is called a pentagon, and so on. A polygon with \( \small n \) vertices is called a \( \small n- \)gon.

Figure 1 shows different types of polygons.

Designation of a polygon

Designate a polygon with letters at its vertices. A polygon is called by alternating letters at its vertices clockwise or counterclockwise. For example, the polygon in Figure 2 is called \( \small A_1A_2A_3A_4A_5A_6 \) or \( \small A_6A_5A_4A_3A_2A_1 \).

Neighboring vertices of a polygon

The vertices of a polygon are called neighboring if they are the ends of one of its sides.

In Figure 2, the vertices \( \small A_2 \) and \( \small A_3 \) are adjacent because they are the ends of the side \( \small A_2A_3. \)

Adjacent sides of a polygon

The sides of a polygon are called adjacent if they have a common vertex.

In the figure 2, the sides \( \small A_4A_5 \) and \( \small A_5A_6 \) are adjacent, since they have a common vertex \( \small A_5. \)

A simple polygon. Self-intersecting polygon

A polygon is called simple if its non-adjacent sides have no common points (internal or end points).

Figure 3 shows a simple polygon because the sides of the polygon do not have self-intersections. And in Figure 4, the polygon is not simple, since the sides \( \small A_1A_4 \) and \( \small A_2A_3 \) intersect. Such a polygon is called a self-intersecting polygon.

Convex polygon

The polygon is called convex if it lies on one side of a straight line passing through any of its sides.

In Figure 5, the polygon lies on one side of the lines \( \small m, \ n, \ l, \ p, \ q, \ r\) passing through the sides of the polygon.

In Figure 6, the line \( \small m\) divides the polygon into two parts, i.e. the polygon does not lie on the same side of the line \(\small m\). Hence the polygon is not convex.

Regular polygon

Simple polygon called is correct if all its sides are equal and all angles are equal. For example, an equilateral triangle is a regular polygon because all its sides are equal and all its angles are 60°. A square is a regular polygon because all its sides are equal and all its angles are 90°.

Figure 7 shows a regular polygon (pentagon), since this polygon has all sides equal and all angles equal. The polygon (rhombus) in Figure 8 is not correct, since all sides of the polygon are equal, but all the angles of the polygon are not equal to each other. The rectangle is also not a regular polygon, because despite the fact that all the corners of the rectangle are equal, but all four sides of the rectangle are not equal to each other.

Star polygon

A self-intersecting polygon with all sides equal and all angles equal is called star or regular star .

Figure 9 shows a stellated pentagon since all angles \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) are equal and all sides are equal: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Perimeter of a polygon

The sum of all sides of a polygon is called perimeter polygon. For a polygon \( \small A_1A_2…A_{n-1}A_n \) the perimeter is calculated from the formula: A_nA_1 \)

Angle of a polygon

The angle (internal angle) of a polygon at a given vertex is the angle between two sides of the polygon converging to this vertex. If the polygon is convex, then all angles of the polygon are less than 180°. If the polygon is non-convex, then it has an interior angle greater than 180° (angle \( \small A_3 \) in Figure 2).

Outer corner of a polygon

The outer corner of a polygon at a given vertex is the angle adjacent to the inner corner of the polygon at a given vertex.

In Figure 10, angle 1 is the outer corner of the given polygon at the vertex \( \small E. \)

Diagonal of the polygon. Number of diagonals

Diagonals are segments connecting two non-neighboring vertices of a polygon.

Let’s derive a formula for calculating the number of diagonals of a polygon.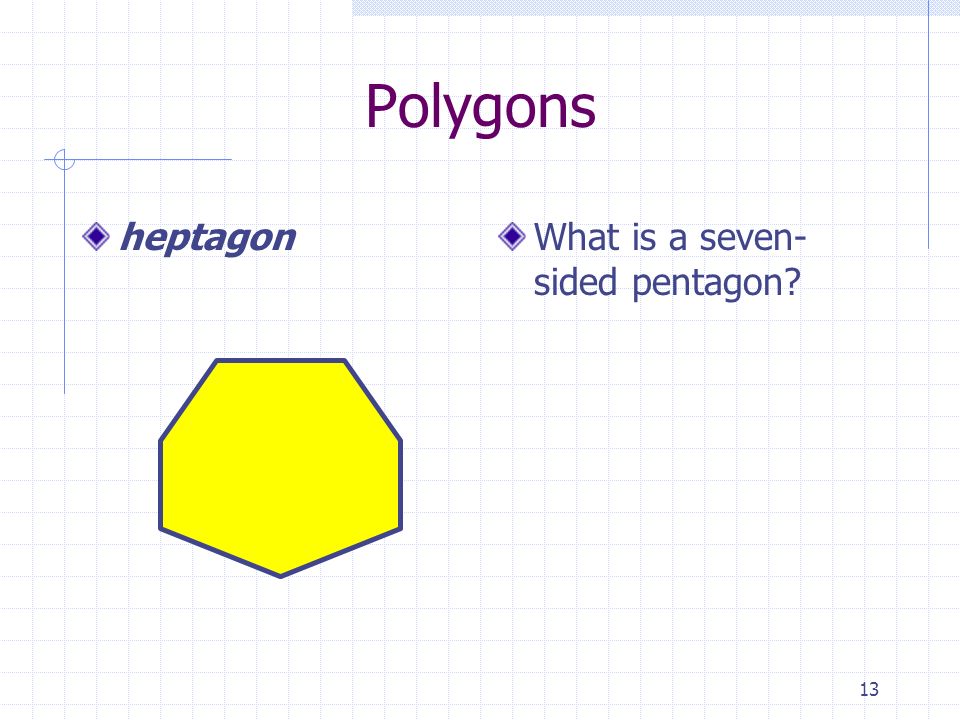 Let a \( \small n \)-gon be given. We choose one vertex of the polygon and mentally draw all the segments connecting this vertex with the other vertices. We get \( \small n-1 \) segments. But since two vertices for the selected vertex are adjacent, and by definition a diagonal is a segment connecting non-neighboring vertices, then from \( \small n-1 \) we subtract 2. We get \( \small n-3 \). Total \( \small n \) vertices. Therefore, the number of calculated diagonals will be \( \small n(n-3). \) Given that each diagonal is a segment connecting two vertices, it turns out that we calculated each diagonal twice. Therefore, the resulting number must be divided by two. Get the number of diagonals of a \(\small n-\)dimensional polygon:

The sum of the angles of a convex polygon

Let’s derive the formula for calculating the sum of the angles of a convex polygon. To do this, draw from the vertex \( \small A_1 \) all the diagonals of the polygon \( \small A_1A_2…A_{n-1}A_n \) (Fig. 11):

The number of diagonals drawn from one vertex, as we found out from the previous paragraph is \( \small n-3 \). Therefore, these diagonals divide the polygon into \( \small n-3+1=n-2 \) triangles. Since the sum of the angles of a triangle is 180°, we get that the sum of the angles of a convex polygon is: \( \small 180°(n-2). \)

\( \small 180°(n-2), \)

(1)

where \( \small n \) is the number of sides (vertices) of the convex polygon.

Angle of a regular polygon

Since all angles of a regular polygon are equal, using formula (1) we obtain the angle of a regular polygon: n} \cdot 180°, \)

where \( \small n \) is the number of sides (vertices) of a regular polygon.

Polygons. Convex polygon. Quadrilateral grade 8 online training at Rostelecom Lyceum

Polygons.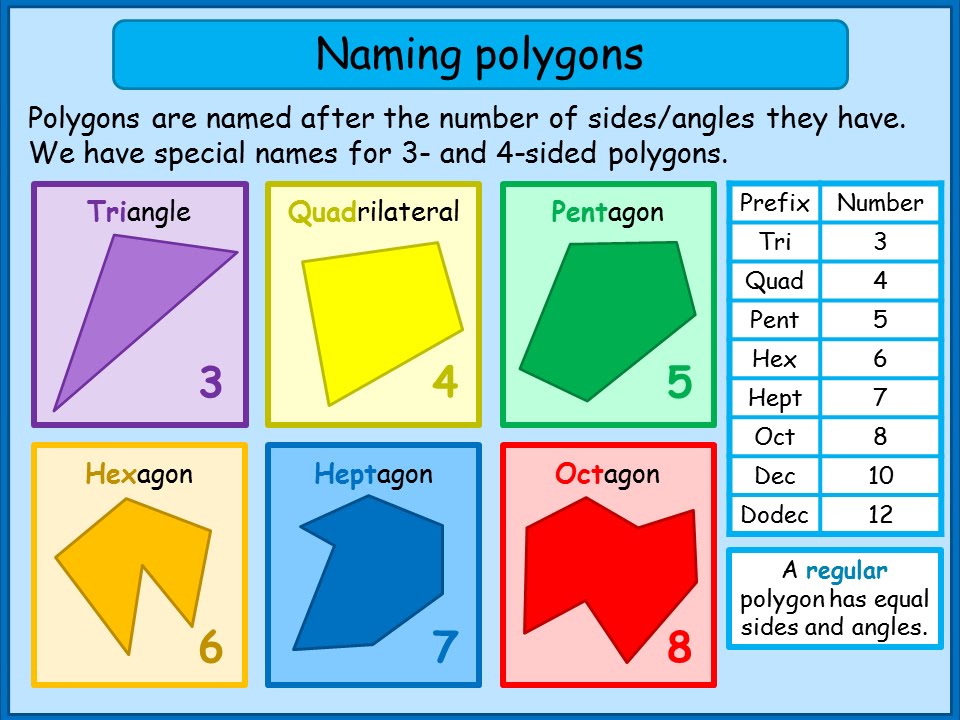 Convex polygon. Quadrilateral.

A triangle is a special case of a polygon.

The name itself already emphasizes that this is a figure that has three corners. Therefore, there can be many of them in a polygon, i.e. more than three. For example, let’s draw a pentagon — a figure with five corners.

Polygon — a figure consisting of several points (more than two) and the corresponding number of segments that connect them in series. These points are called vertices of the polygon, and the segments are called sides . In this case, no two adjacent sides lie on the same straight line and no two non-adjacent sides intersect.

Any polygon divides the plane into two regions: internal and external. The inner area is also referred to as a polygon.

In other words, for example, when talking about the pentagon A ₁ A ₂ A ₃ A ₄ A ₅ , they mean both its entire inner region and its border. And the inner region includes all points that lie inside the polygon.

Polygons are sometimes called n-gons to emphasize that we are considering the general case of having some unknown number of corners (n pieces).

Perimeter of a polygon is the sum of the lengths of the sides of the polygon.

The line segment connecting any two opposite vertices is called the diagonal of the polygon.

Polygons are divided into convex and non-convex . For example, the polygon shown in the figure above is convex, while the figure below is non-convex.

A polygon is called convex if, when a line is drawn through any of its sides, the entire polygon lies only on one side of this line. All other polygons are non-convex.

Regular polygon is a convex polygon with all sides and angles equal.

The essential difference between a quadrangle and a triangle is that it can be convex or non-convex.

A very important difference that every carpenter knows is that a triangle is a «rigid» figure, while a quadrilateral (like all other polygons) is «non-rigid».

A triangle cannot be reshaped without changing the side lengths. At the same time, for any quadrilateral, you can change its shape without changing the length of the sides. In practice, this will mean that a triangle knocked together from three planks will be rigid, will not be crushed even under strong influences, and a quadrangle will change its shape with sufficient load from the side.

To describe the properties of polygons, there are two most important theorems about their angles: the theorem on the sum of the interior angles of a convex polygontheorem on the sum of the exterior angles of a convex polygon.