Geometry shape names 3d: General Data Protection Regulation(GDPR) Guidelines BYJU’S
Posted on3D Shapes Names, 3D Shapes and Their Names
3D Shapes Names, 3D Shapes and Their Names
Table of Contents
Toggle
3d Shapes Names
In this lesson, we will examine the subject of ‘3d shapes names’ closely. 3d shapes names is an issue that we may encounter in daily life. 3d shapes names are general:
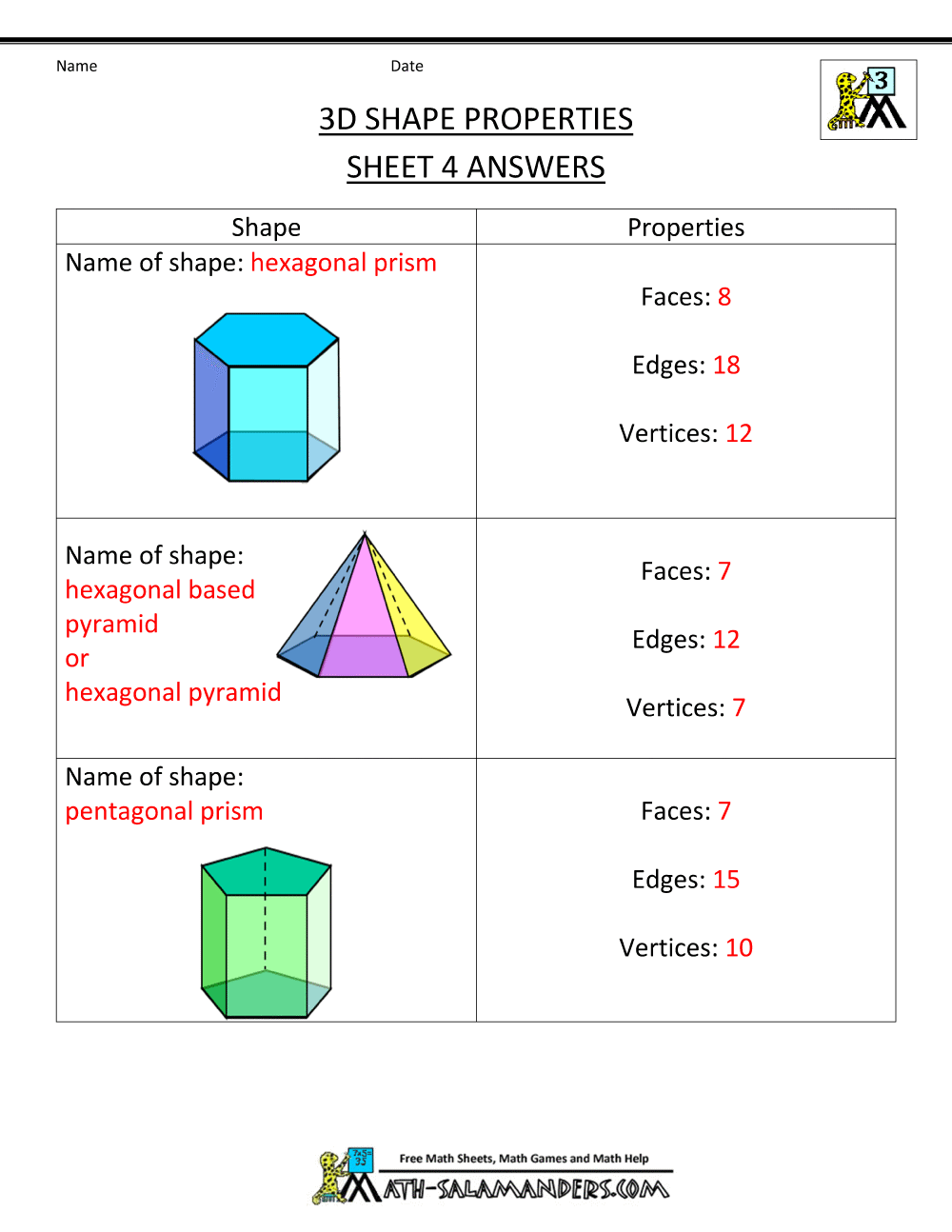
Cylinder
It is the object bounded by two parallel surfaces that vertically cut the axis of an object whose bottom and top bases consist of circles equal to each other. In other words, it is a geometric 3d shape formed by a circle making a non-planar translation movement. If the direction of movement is perpendicular to the circle, the resulting roller is called a perpendicular roller, if not, an oblique roller.
- The roller used in the industry for thinning metals, polishing fabrics, printing on paper, printing and compressing something it passes on, is in the form of a cylinder.
Here are 2d Shapes and Their Names, Definition and Examples with Pictures
Cube
Cube is a three-dimensional geometric 3d shape consisting of six squares whose areas are equal to each other with right angles. It is also referred to as smooth six-sided and is one of 5 platonic bodies. The most important feature of the cube is that all faces are square. Its volume is found by multiplying 3 equals.
- The object whose opposite sides are equal and the areas of all faces are equal are named as cubes.
Oid Cuboid
In geometry, a cuboid is a convex polyhedron bounded by a six quadruple face whose polyhedron is the same as that of a cube.
- The topic of cuboid told at school has been my most challenging lesson lately.
Cone
Cone is a geometric 3d shape created by the line segments that connect every point of a circle in a plane to a point outside the plane in mathematics. The cone obtained by turning the right triangle around a right edge is called a steep cone or a rotary cone.
- The cone is an end-pointed geometric object, which is interestingly formed by the point where each point on the circular plane is outside the circle of the circle and is usually combined with a point in the center.
Pyramid
The pyramid is an n-edged polyhedron seated on a n-pointed polygonal base to merge triangular surfaces on a single hill.
- All of the architectural structures built by the ancient Egyptians as royal tombs, square-shaped, triangular sides with a typical masonry uniting at the top are all examples of pyramid shape.
Sphere
With its daily use, the sphere is a geometric object with a perfect symmetry, it is a surface; lies in three-dimensional Euclidean space. In everyday use, a solid object is called a sphere.
- The line connecting the two points of the sphere and passing through the center constitutes the diameter of the sphere.
Hemisphere
Hemisphere or hemisphere is the name given to each of the halves in the east and west when it is assumed that the earth is divided by the equator by the equator, with its longitudinal halves in the north and south.
- Since the earth is not a full sphere but a geoid, the hemispheres of the world are not a full geometric hemisphere.
Triangular prism
Since prisms are named according to the shape of their bases, prisms with a triangular base are called triangular prisms.
- In geometry, the triangular prism is a triangular base, a three-sided prism, a polyhedron consisting of a translated copy and 3 faces connecting the corresponding sides.
Equilateral Triangular Prism
The bases of the equilateral triangular prism are equilateral triangles. Its side surfaces consist of three identical rectangles.
- The teacher gave additional lessons on the subject of equilateral triangular prism.
Right Triangular Prism
The base of the right triangular prism is a right triangle. Side surfaces consist of three rectangle.
- All objects with steep triangular prism-style shapes attract my attention.
Hexagonal prism
The hexagonal prism has many faces, the sides of which are rectangular with two bases, one at the bottom and one at the top.
- Hexagonal prism is a shape that I do not give up in all the paintings I make.
Torus
It is a bagel surface in topology and geometry. It is obtained by rotating a circle in three-dimensional space around a line lying on the same plane and not touching the circle. The surface of the bagel or the inflated bladder used for swimming is mathematically a bagel. The shape of the torus is also formulated as a mathematical pattern. The shape of an apple and a torus is known as the torus. The shape of the torus is present on many units containing life.
There is a torus pattern on the rotation of the earth, planets, solar system, plane, flying saucer and atom. It is accepted by some scientists that the shape of the universe is also in the torus model. The energy in the Torus pattern flows to one end by circling around the center and exits from the other end.
- The energy system that Tesla found and sabotaged by the Industrialist Morgan was prepared according to the torus model.
Pentagonal Prism
Pentagonal Prism is a type of prism whose bases are pentagonal. They consist of two peers and parallel bases. It has two types as oblique and steep. Side faces are parallel edges in oblique prisms, side faces are rectangular or square in upright prisms.
- The shape we created as a result of the combination of 5 rectangles and 2 pentagons is called Pentagonal Prism.
Ellipsoid
The ellipsoid is a second order surface and its intersection is ellipse with any plane. It has a symmetrical shape with respect to three axes perpendicular to each other called prime axes and the center of these axes.
- An egg with an elliptical cross section is an example of an ellipsoid.
Three Dimensional Shapes (3D Shapes)
What Are Three Dimensional Shapes?
In geometry, a three dimensional shape can be defined as a solid figure or an object or shape that has three dimensions— length, width, and height. Unlike two dimensional shapes, three-dimensional shapes have height, which is the same as thickness or depth. Three dimensional is also written as 3D and hence, these figures are commonly called 3D shapes too. All three dimensional figures occupy space, which is measured in terms of volume.
In 3D shapes, 3D refers to three-dimensionality. Dimensions can usually be thought of as measurements in a direction. Length, width, and depth can be considered dimensions.
Related Games
History of 3D Shapes
All 3D shapes have three measurements: length, width, and height. Shapes look different from different directions. All 2D shapes are only measured by their length and width.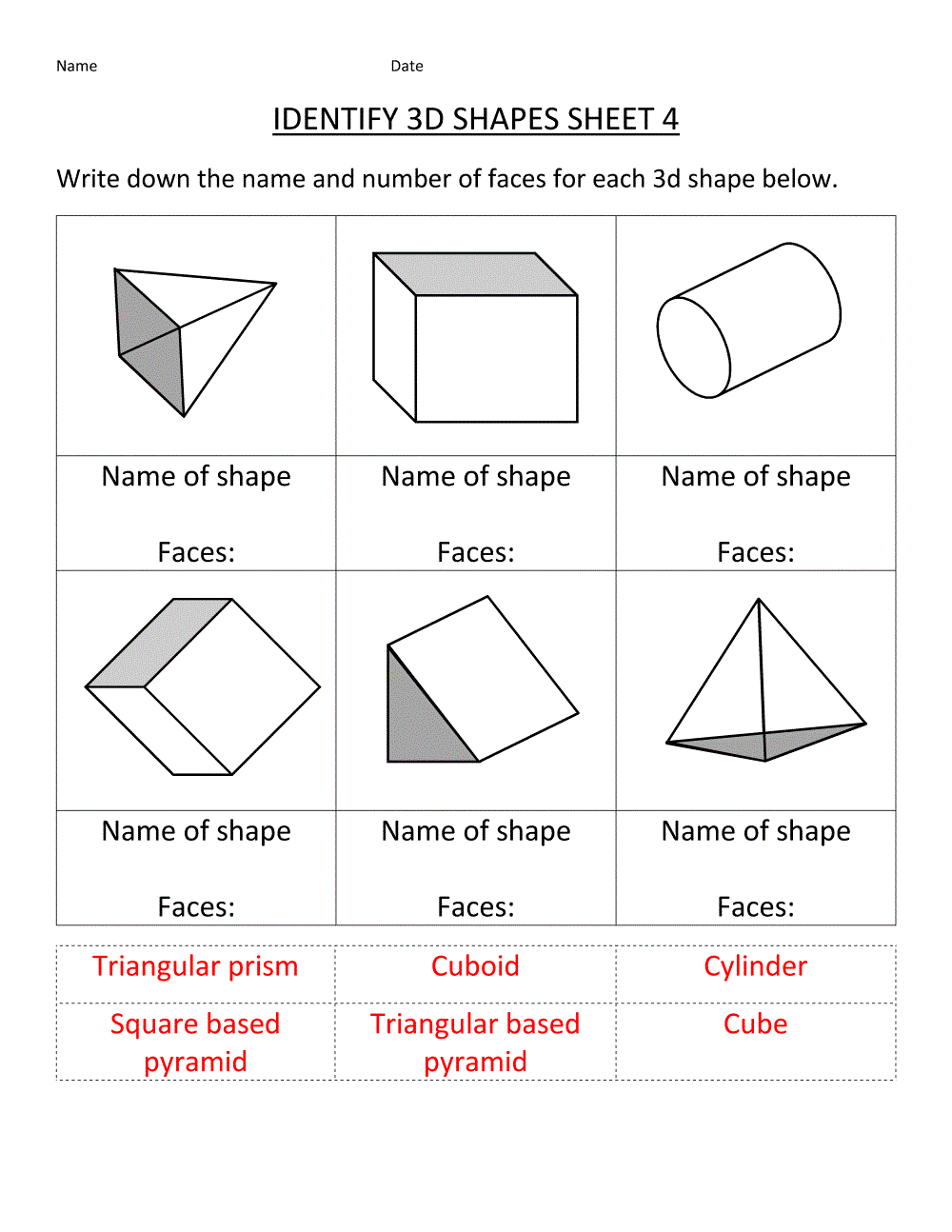
By convention, the first three dimensions are represented as spatial dimensions x-y-z. Width, height, and depth are their respective names.
Related Worksheets
Examples of Three Dimensional Shapes
A cube, rectangular prism, sphere, cone, and cylinder are the basic three dimensional figures we see around us.
Real-life Examples of Three Dimensional Shapes
3D shapes can be seen all around us. We can see a cube in a Rubik’s Cube and a die, a rectangular prism in a book and a box, a sphere in a globe and a ball, a cone in a carrot and an ice cream cone, and a cylinder in a bucket and a barrel around us.
Some real-life examples of 3D shapes are listed below:
- Cone: Traffic cones and birthday caps are cone-shaped.
- Triangular prism: A tent is the shape of a triangular prism.
- Square pyramid: The pyramid of Giza in Egypt is the shape of a square pyramid.
- Rectangular prism: Boxes such as shoe boxes and cereal boxes are shaped like rectangular prisms.
Attributes of Three Dimensional Shapes
There are three attributes of a three dimensional figure: face, edge, and vertex. Let’s understand three dimensional shapes and their properties in detail.
Face: Each single surface, flat or curved, of the 3D figure is called its face.
Edge: The line, where two faces of the 3D figures meet, is called its edge.
Vertex: Each corner, where three faces of 3D figures meet, is called its vertex. Vertices are the plural of the vertex.
List of Three Dimensional Shapes
Here’s a list of the names of three dimensional shapes with their pictures, and attributes.
Sphere
All the points on a sphere are at the same distance from its center.
- It is perfectly symmetrical and shaped just like a ball.
- It also has length besides radius, diameter, circumference, volume, and area.
- The distance from the center to every point on the surface of a sphere is equal.
- No edges or vertices are found on its one face.
- Since it does not have a flat face, it is not a polyhedron.
Cube and Cuboid
A cube and a cuboid are both big blocks. The difference between them is that a cube has square faces, while a cuboid has rectangular faces.
Cylinder
A cylinder has two circular faces on both its ends and one curved surface along its length. It has height and radius. A cylinder’s height is perpendicular to its surface, from top to bottom.
- The face of a cylinder is curved.
- From the bottom to the top, its shape remains the same.
- Two identical ends shape the object’s three-dimensional form. The ends can be round or oval.
- A right cylinder has the centers of its circular bases along the same line, while an oblique cylinder has the centers of its bases along different lines.
Formula of Three Dimensional Shapes
Net of Three Dimensional Shapes
A net is a pattern made when the surface of a 3D figure is laid out flat, showing each face of the figure.
3D figures can have more than one net pattern. A few 3D shapes names and their nets are shown below:
Fun Facts:
All three dimensional shapes are made up of two dimensional shapes.
Difference between 2D Shapes and 3D Shapes
Let’s differentiate between 2D and 3D shapes by understanding two dimensional and three dimensional shapes and their properties.
Solved Examples of Three Dimensional Shapes
Example 1: Which of the following is a 3D shape?
Cone Square Sphere Cuboid Cylinder Parallelogram
Solution:
Cone Sphere Cuboid Cylinder
Example 2: State whether the following are true or false.
- A three-dimensional shape has 3 dimensions.
- Three-dimensional shapes are also called flat shapes.
- Three-dimensional shapes occupy space.
- All three-dimensional shapes have flat faces.
Solution:
- True
- False. Three-dimensional shapes are also called solid shapes.
- True
- False. Sphere is a three-dimensional shape with no flat face.
Example 3: Complete the table with attributes of the 3D shapes listed.
Solution:
Example 4: Match the object with its shape.
Solution:
- (a) – (iii)
- (b) – (i)
- (c) – (iv)
- (d) – (ii)
Example 5: Calculate the surface area of a cuboid with a width of 4 units, length of 3 units, and height of 5 units.
Solution:
Given, the cuboid has three units of length, four units of width, and five units of height.
Surface area of the cuboid $= 2 \times (\text{lw} + \text{wh} + \text{lh})$ square units
$= 2 \times (\text{lw} + \text{wh} + \text{lh})$
$= 2[(3 \times 4) + (4 \times 5) + (3 \times 5)]$
$= 2(12 + 20 + 15)$
$= 2(47)$
$= 94$ square units
Therefore, the surface area of the given cuboid is 94 square units.
Example 6: Jane likes to drink milk from a cylinder-shaped glass. Her glass has 15 units of height and 3 units of base radius. How much milk can she fill in the glass?
Solution:
Given that the height of the glass is 15 units, and the radius of the base is 3 units.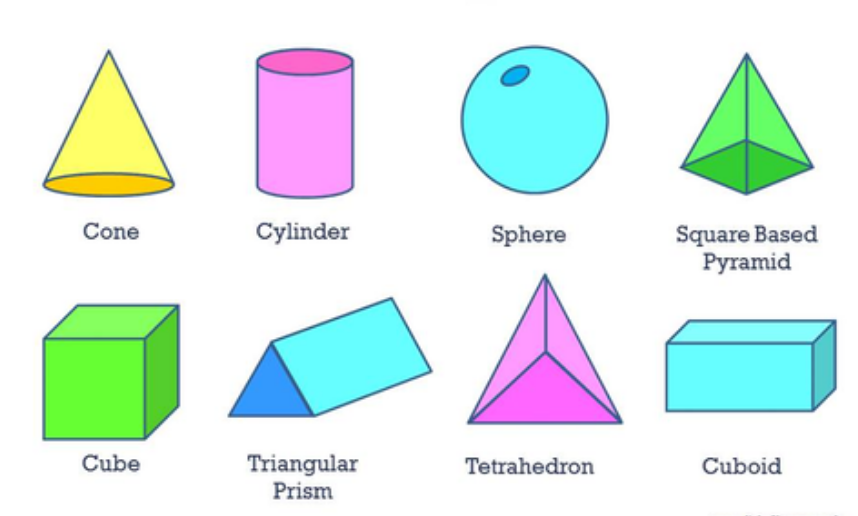
Therefore, Jane can fill approximately 424 cubic units of milk in her glass.
Practice Problems of Three Dimensional Shapes
1
Which shape has 2 flat faces and one curved face?
Cylinder
Sphere
Cone
Cuboid
Correct answer is: Cylinder
Cylinder has two flat faces which are a circle in shape and one curved face.
2
How many square shapes does the net of a cube have?
4
6
8
10
Correct answer is: 6
Cube has 6 faces that are squares. So, the net of the cube will have 6 square shapes.
3
Which of the following has no edge?
Cone
Cylinder
Cuboid
Sphere
Correct answer is: Sphere
Sphere has one face. So it has no edge.
4
Which of the given shapes is NOT a 3D shape?
Trapezoid
Prism
Pyramid
Cube
Correct answer is: Trapezoid
Trapezoid is a 2D shape with four sides with one pair of opposite sides parallel to each other and the other two sides of it are non-parallel.
5
What is the intersection of two faces of a solid figure called?
Vertex
Side
Face
Edge
Correct answer is: Edge
Edges are the line segments that connect two faces. The faces of the cube intersect at lines called edges. Figures with multiple edges are called solid figures. The intersection of several planes is called a vertex.
6
Three-dimensional geometric figures are called ________.
shapes
solids
faces
polygons
Correct answer is: solids
Three-dimensional geometric figures are called solids.
7
In mathematics, what is a solid, pointed figure joined to a vertex by a curved surface with a flat, round base?
Cone
Sphere
Cylinder
Pyramid
Correct answer is: Cone
Cones are three-dimensional solids made up of a circular base joined to a single point (called the vertex) by curved sides. Alternatively, you can think of a cone as a circular pyramid.
Frequently Asked Questions of Three Dimensional Shapes
What are the different types of 3D figures?
Cube, cuboid, cylinder, sphere, cone, prism, and pyramids.
What are the attributes of three-dimensional shapes?
Three-dimensional shapes have 3 dimensions—length, width, and depth. As a result of these dimensions these shapes have attributes of faces, edges and vertices.
What is an edge?
An edge is a line where two faces of a three-dimensional shape meet.
For example, a cube has 12 edges.
What are vertices?
Vertices are corners where three faces meet. For example, a cuboid has 8 vertices.
What is the use of volume of a three dimensional shape?
Volume helps to find the space occupied by the given shape.
A cube net is made up of how many squares?
A cube net is made up of six squares.
Creative trident. Visual geometry with Cabri 3D — Teacher’s newspaper
You won’t surprise anyone with a computer in a mathematics lesson. True, despite the abundance of electronic materials, interesting and useful applications are still not enough.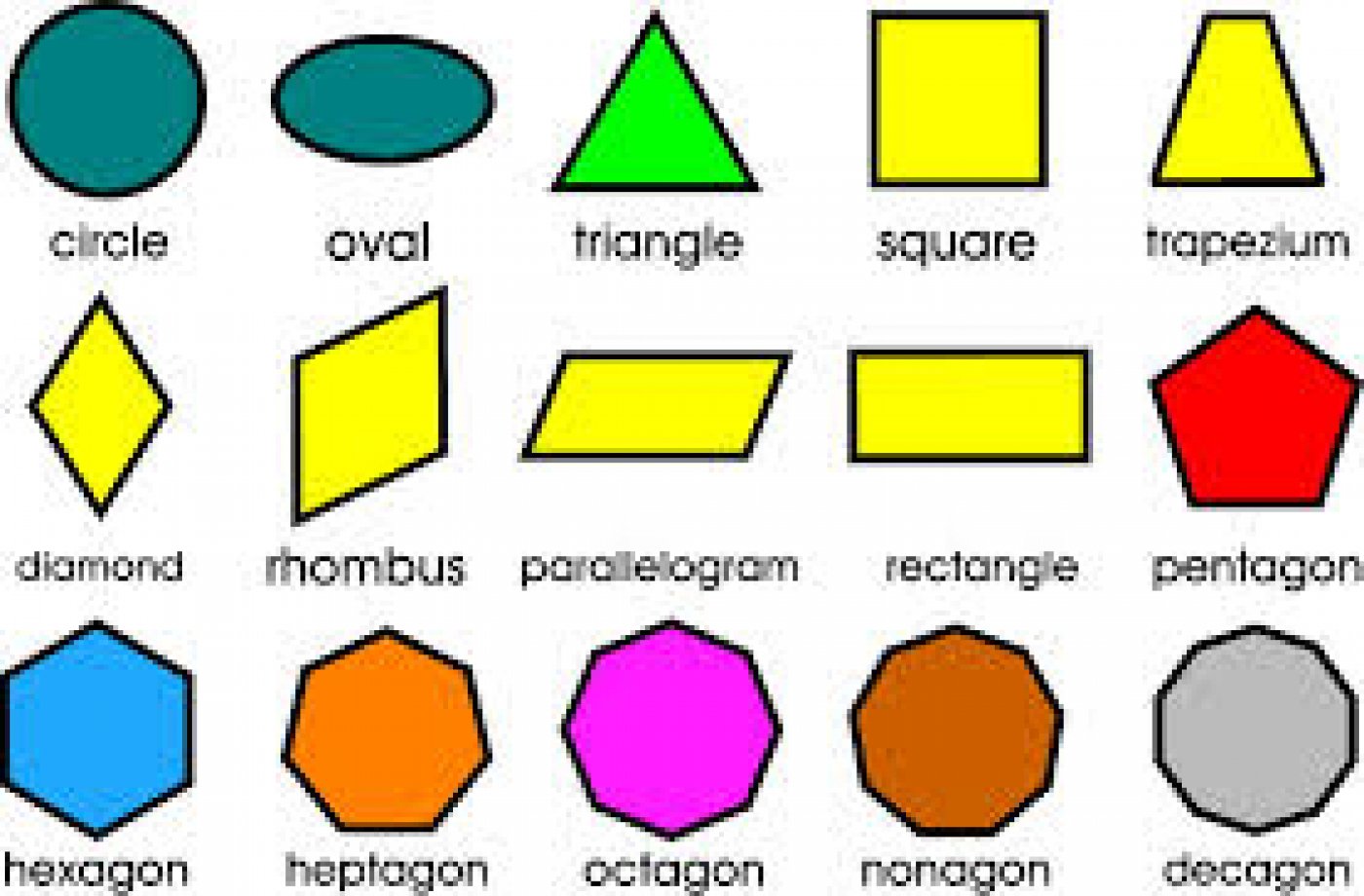
The entire publication is in PDF format: Download/View (Viewing requires Adobe Reader or any equivalent).
On the Internet at www.cabri.com you can download a wonderful program with the same name, which can work wonders. But about the program a little later, but for now let’s remember the traditional lessons of the 7th grade, in which students get their first ideas about geometry.
The beginnings of planimetry: the simplest figures, axioms, theorems. Like a snowball, more and more new concepts are accumulating, penetrating into the unprepared consciousness of a schoolchild. Chalk, ruler and board, on which, out of nowhere, appear angles, triangles, circles and other geometric shapes. The blackboard is a faithful assistant to the teacher, like a stern guard, it limits children’s perception to a single fixed plane.
Where is the space? After all, initially the child acquires his life experience in it.
Perhaps, school planimetry should be more often correlated with space (at least virtual), in which amazingly beautiful, perfect and voluminous figures “live”. True, it is difficult to draw such “residents” on the blackboard, unless, of course, you are an artist and a professional draftsman. So, you just need to use the right program.
The computer program Cabri3Dv2, like an original and industrious master, can do everything: draw colorful pictures consisting of spatial and flat figures; rotate them in space; perform various symmetrical constructions; turn bodies into sweeps; build all kinds of projections; create architectural masterpieces from combinations of geometric shapes. Numerous actions occur quickly, dynamically and visually!
Opening a new file, a plane appears on the screen, in which the “tridental basis of the Cartesian space” is placed in the most prominent place — length, width and height (later students will learn that its parts are unit coordinate vectors).
We mark a point on the plane, then the second, and then a straight line appears. Based on a visual picture, it is easy to build a dialogue with the class (Fig. 1). Where is the line located? What points define it? What parts does it divide the plane into? Which vertices of the triangle lie in different half-planes? Why?
Do you recognize? Yes, these are the questions we ask in the lesson, presenting the material of one of the program topics of school geometry.
The restless moving plane not only bears familiar figures, but gives rise to more and more new ones. Here we see a ball familiar from childhood — a sphere. Let’s cut it with a plane, and a circle will appear (Fig.
It is easy to build anything in the starting plane. We need some figure — we build a figure, a combination of them is required — the computer will draw it instantly (Fig. 3). And then you can supplement the drawing by drawing the elements of the resulting combination. Did you need a drawing for some task or do you need to come up with a task based on the finished drawing? Cabri3D will help in this case too! Its coordinate trident lies in the plane and generates forms, guarding the two-dimensional realm of geometric figures.
The program is also indispensable in high school, when geometry passes into space. When building on a school board, complex drawings require a lot of time and effort. On the computer — faster and easier, and most importantly, brighter and more diverse. Points, straight lines, planes are born before the eyes of students (Fig.
Gradually spatial figures take on new forms, there is a progressive development of the imagination, intuition and fantasy of students. Tasks become more complex, new configurations appear. The computer helps visualize combinations of figures, their sections by planes, reveals the properties and dependencies between elements (Fig. 6), realizing the most incredible ideas of students and teachers. With the help of this program, for almost every lesson, you can prepare a presentation in advance for a particular educational goal. It is not difficult to make a chain of slides: copy the designed drawings, select a set of questions and tasks — and here is an interactive tutorial that can be used in more than one geometry lesson.
The program is useful not only at the lesson, but also at an additional lesson, circle, elective. Indeed, if you need to talk about the complete filling of space using polyhedra, then again you can use Cabri3D.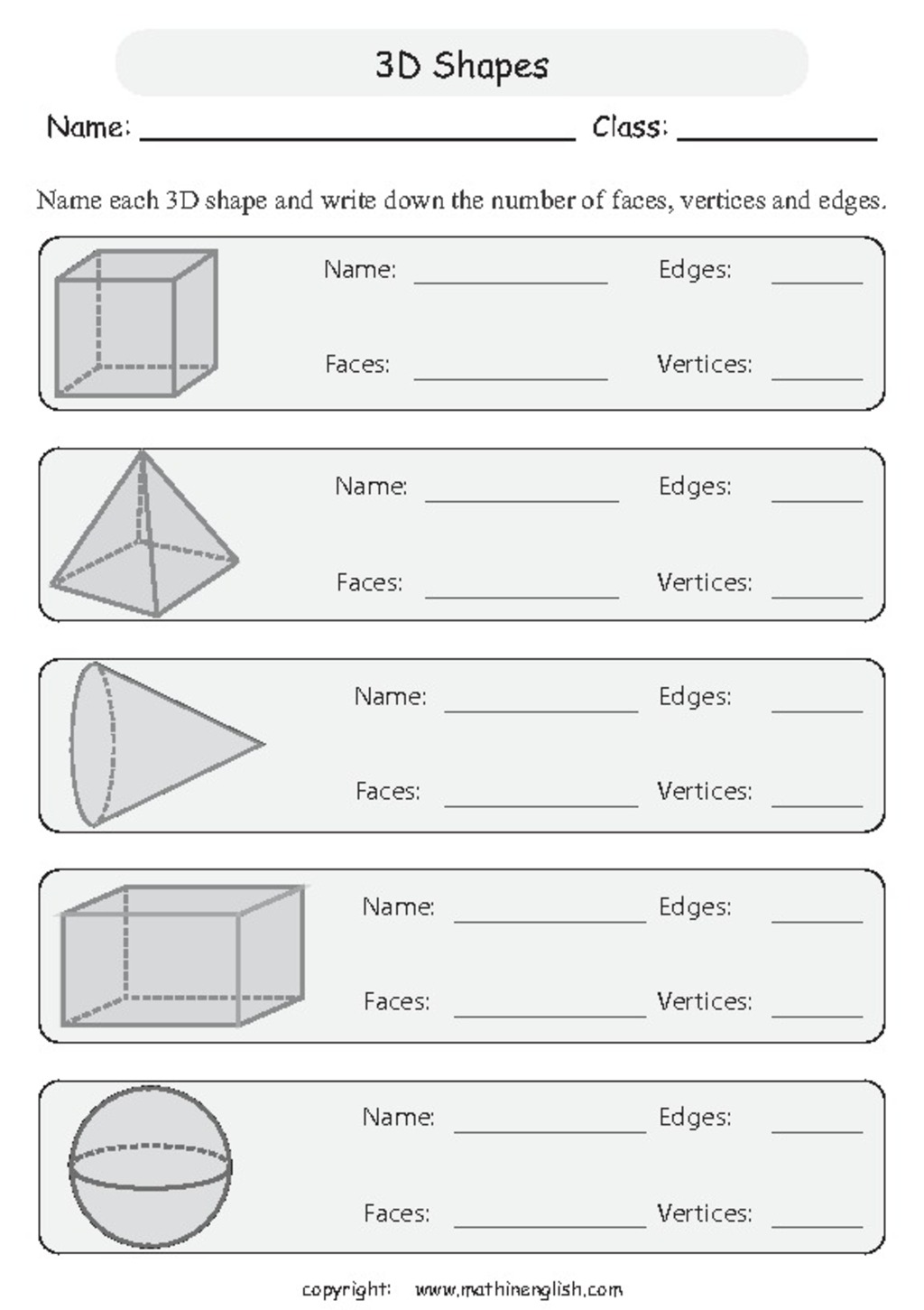
If you go to the website of the German professor Heinz Schumann (www.mathe-schumann.de), who has been using this program brilliantly for many years, then a lot of all kinds of geometric models will open. Modeling figures is very important for studying school geometry. This site has a video clip that explains in detail how to work in the program. Open the link http://www.mathe-schumann.de/geometrie-seite/videoclips.html, watch, study and create lively, beautiful and visual geometry with your students in the classroom.
Aleksey AZEVICH, Associate Professor, Department of Informatization of Education, Moscow State Pedagogical University, Moscow
geometry — How to calculate a uniform increase in a complex 3D figure
Question asked
Changed
6 years 2 months ago
Viewed
367 times
Good afternoon, there is some abstract 3D object of complex geometry.
Let’s say its volume is V₁ cubic meters.
The task is to calculate the amount (shown in yellow in the illustration) by which each vertex of the object must be shifted in order to obtain an object with a new volume V₂.
Is there any formula to find this value?
In the English segment, this operation is called offset.
- 3d
- geometry
- objects
- three.js
- formulas
10
Disclaimer: with three.js didn’t work.
New position for each vertex:
(kx, ky, kz). Where k = cube_root_of(V2/V1)
That is, the coordinates of each vertex must be changed to
((k - 1)x, (k - 1)y, (k - 1)z)
And then shift all the coordinates so that, for example, the centers of gravity of the old and new figures coincide, or the circumscribing box expands/shrinks uniformly in the directions of the coordinate axes.
But this already depends on additional conditions of the problem not included in the question.