Right angled scalene triangle: General Data Protection Regulation(GDPR) Guidelines BYJU’S
Posted onRight Scalene Triangle — Properties, Definition, Formula, Examples
LearnPracticeDownload
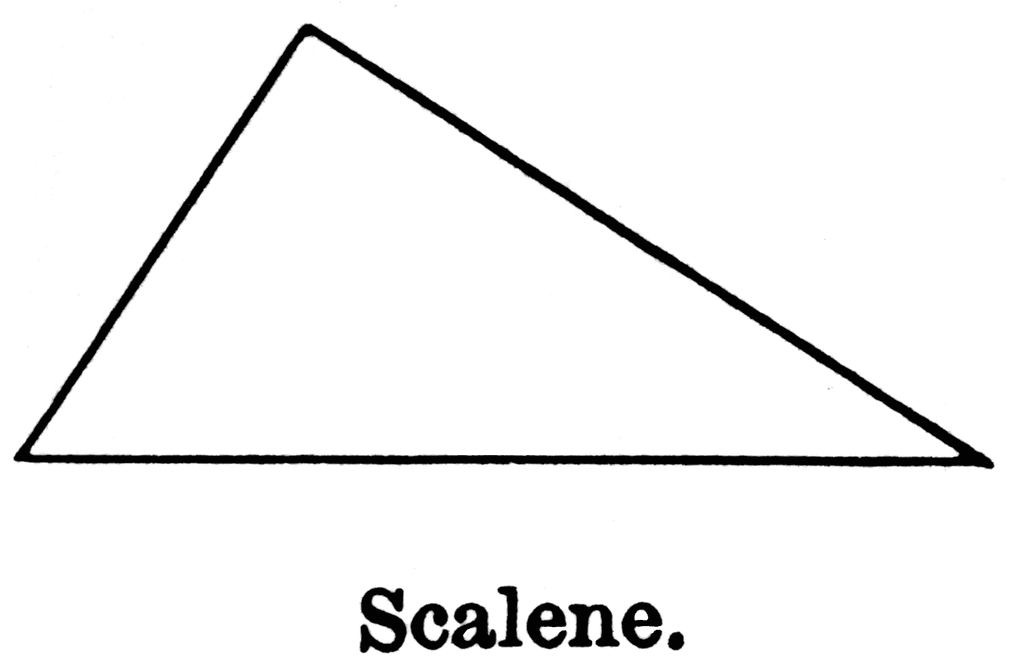
A right scalene triangle is a triangle in which all three sides are different in length and one angle is equal to 90 degrees. A triangle is a closed figure made up of three lines and three angles. There are different types of triangles based on the side lengths and angles like a right triangle, scalene triangle, equilateral triangle, etc. A right scalene triangle is one such type of triangle that contains the properties of a right triangle and a scalene triangle.
| 1. | What is a Right Scalene Triangle? |
| 2. | Properties of a Right Scalene Triangle |
| 3. | Right Scalene Triangle Formulas |
| 4. | FAQs on Right Scalene Triangle |
What is a Right Scalene Triangle?
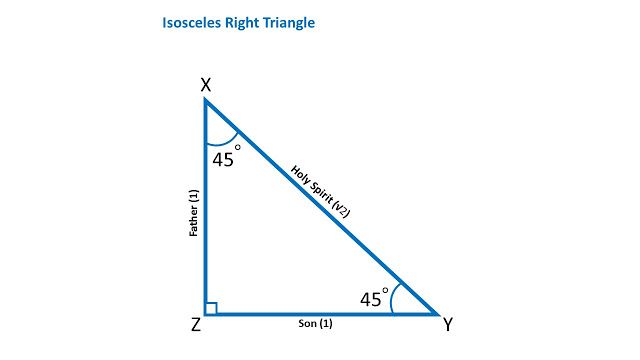
In geometry, a right scalene triangle can be considered as the triangle that contains the properties of both a right triangle and a scalene triangle. Let us recollect the meaning of right triangles and scalene triangles.
- A right triangle is one in which one interior angle measures 90° and the other two angles are acute angles (less than 90°). There are three sides whose lengths share the following relationship: Hypotenuse2 = Perpendicular2 + Base2.
- A scalene triangle is one in which all three sides and angles are different in measurements. There is no specific relationship between the side lengths.
Observe the figure given below to understand how a scalene right triangle appears.
Properties of a Right Scalene Triangle
It is easy to identify a right scalene triangle if we know its properties. The properties of the right scalene triangle are listed below:
- All three sides are different in measurements.
- All three angles are different in measurement with one angle of 90°
- The sides of a right scalene triangle share the following relationship: Hypotenuse2 = Perpendicular2 + Base2.
This relationship is known as the Pythagoras theorem.
- The side opposite to the right angle is the longest side known as hypotenuse.
- The sum of all the interior angles is 180°
- A 30-60-90 triangle is a perfect example of a right scalene triangle.
Right Scalene Triangle Formulas
The formula of a right scalene triangle is useful to find the area and perimeter of the triangle. There are two possible formulas that can be used to find the area of a right scalene triangle based on what information is given to us.
- If the length of base and height of the triangle is given, then area = [1/2 × base × height]
- If the length of all three sides are given, then area = √s(s-a)(s-b)(s-c), where ‘s’ is the semi perimeter = perimeter/2 = (a + b + c)/2.
To find the right scalene triangle perimeter, we just need to add the length of all three sides.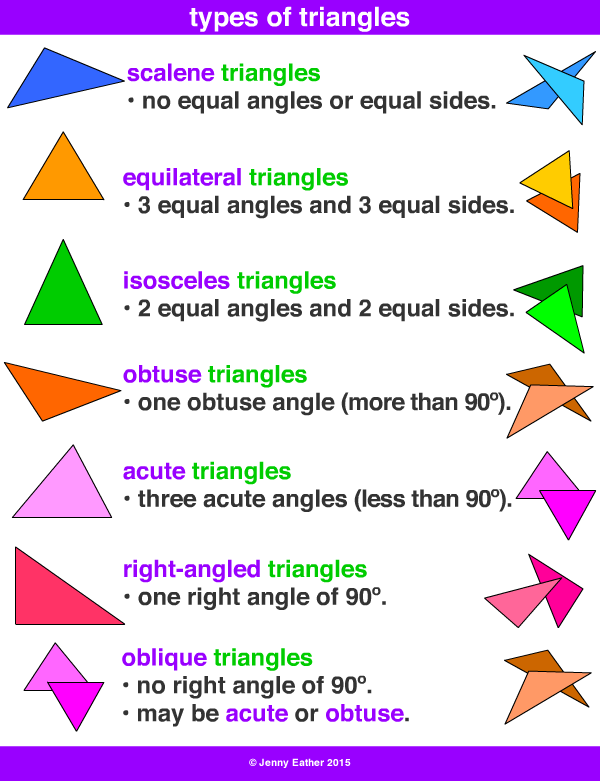
☛ Related Articles
- Area of Scalene Triangle
- Types of Triangles
- Area of Right Triangle
Right Scalene Triangle Examples
-
Example 1: Find the area of a right scalene triangle if the base is 10 units and the height is 8 units.
Solution: Given, base (b) = 10 units and height (h) = 8 units. The formula to calculate the area is 1/2 × b × h. By substituting the values, we get area = 1/2 × 10 × 8.
⇒ Area = 5 × 8 = 40
Therefore, the area of the given right scalene triangle is 40 square units.
-
Example 2: What will be the perimeter of a right scalene triangle if the sides are of lengths 5 units, 12 units, and 13 units?
Solution: The perimeter is the sum of all the sides of a shape.
Here, the given three side lengths are 5 units, 12 units, and 13 units. So, the perimeter = 5 + 12 + 13 units, which is 30 units. Therefore, the perimeter of the given scalene right triangle is 30 units.
-
Example 3: Find the length of the hypotenuse of a right scalene triangle if base = 5 inches and perpendicular = 4 inches.
Solution: The relation between the sides of a right scalene triangle is Hypotenuse2 = Perpendicular2 + Base2. By substituting the values given in the question, we get h2 = 52 + 42.
⇒ h2 = 25 + 16
⇒ h2 = 41
⇒ h = √41 inches
Therefore, the length of the hypotenuse is √41 inches.
go to slidego to slidego to slide
Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.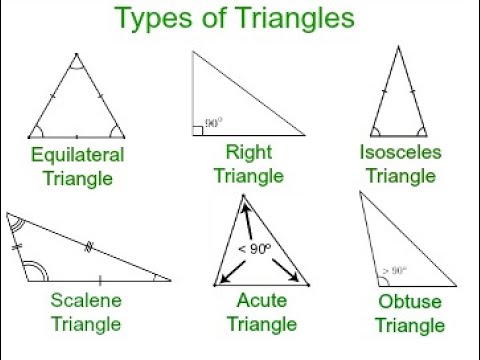
Book a Free Trial Class
Practice Questions on Right Scalene Triangle
go to slidego to slide
FAQs on Right Scalene Triangle
What is a Right Scalene Triangle?
A right scalene triangle is a triangle that contains the properties of both the right triangle and scalene triangle. It comes in the category of both right triangles and scalene triangles. One of its angles measures 90°and all the sides and angles are different in measurements.
What is the Area of a Right Scalene Triangle?
The area of a scalene right triangle can be calculated by using the formula: Area = 1/2 × base × height. The perpendicular of the right scalene triangle can be taken as the height and the side adjacent to it other than hypotenuse is the base.
How to Draw a Right Scalene Triangle?
To draw a right scalene triangle, the first step is to draw two perpendicular line segments of different measurements. Then, we can simply join the opposite ends of both to form a right scalene triangle.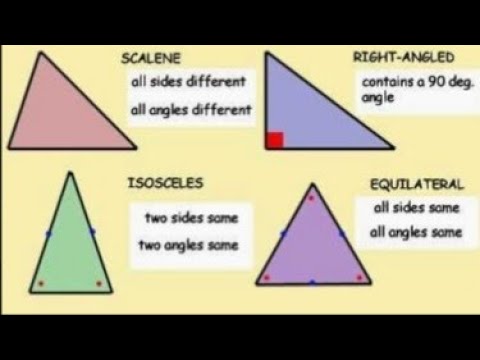
How to Find the Hypotenuse of a Right Scalene Triangle?
The hypotenuse is the longest side of a right triangle which is opposite to the 90-degree angle. To find the length of the hypotenuse, we need to use the following formula which expresses the relation between three sides of a right scalene triangle: Hypotenuse2 = Perpendicular2 + Base2. This formula is known as the Pythagoras theorem.
What does a Right Scalene Triangle Look Like?
A right scalene triangle looks like a right triangle with two perpendicular sides forming an angle of 90 degrees. All the three angles of a right scalene triangle are different in measurement.
How to Find the Angles of a Right Scalene Triangle?
In a right scalene triangle, the sum of both the acute angles is 90° and the third angle is equal to 90°. So, if any one of the acute angles is given, then we can easily find the third angle by subtracting the given acute angle from 90.
Download FREE Study Materials
Right Scalene Triangle Worksheets
Math worksheets and
visual curriculum
Right Angle Scalene Triangle — Formulas and Examples
A scalene triangle with a right angle is called a right angle scalene triangle.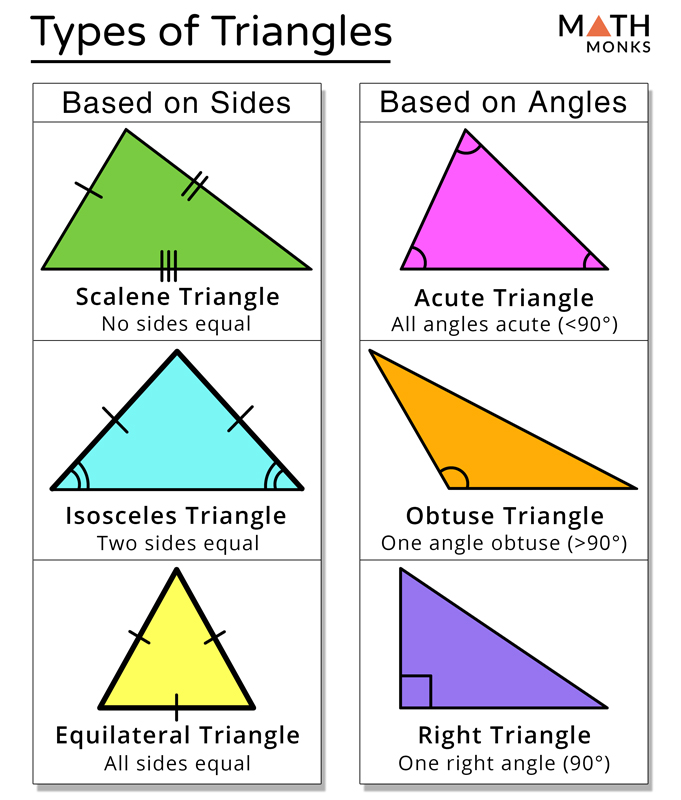
Here, we will learn more about scalene triangles with right angles. We will learn about its characteristics and its most important formulas. In addition, we will use these formulas to solve some exercises.
GEOMETRY
Relevant for…
Learning to find the right angle scalene triangle with examples.
See formulas
Contents
GEOMETRY
Relevant for…
Learning to find the right angle scalene triangle with examples.
See formulas
What are right angle scalene triangles?
Right angle scalene triangles are triangles that are scalene and have a right angle at the same time.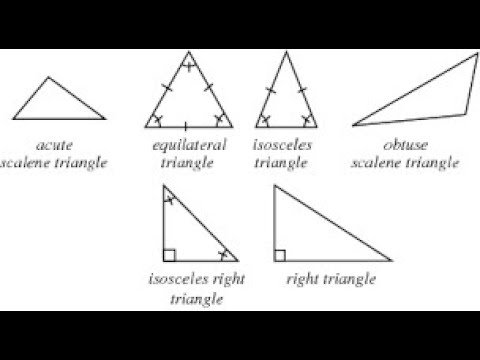
On the other hand, a scalene triangle is a triangle that has all of its sides of different lengths and all of its interior angles of different measures. These triangles share the same main characteristics as all other triangles, that is, the sum of their interior angles is equal to 180 degrees.
The following is an image of a right angle scalene triangle:
Formulas for right angle scalene triangles
The most important formulas for solving problems with scalene triangles with right angles are the area formula, the perimeter formula, and the Pythagorean theorem.
Area of scalene triangles
The area of a scalene triangle can be calculated using the length of its base and its height:
| $latex A=\frac{1}{2}\times b \times h$ |
where, b is the length of the base and h is the length of the height.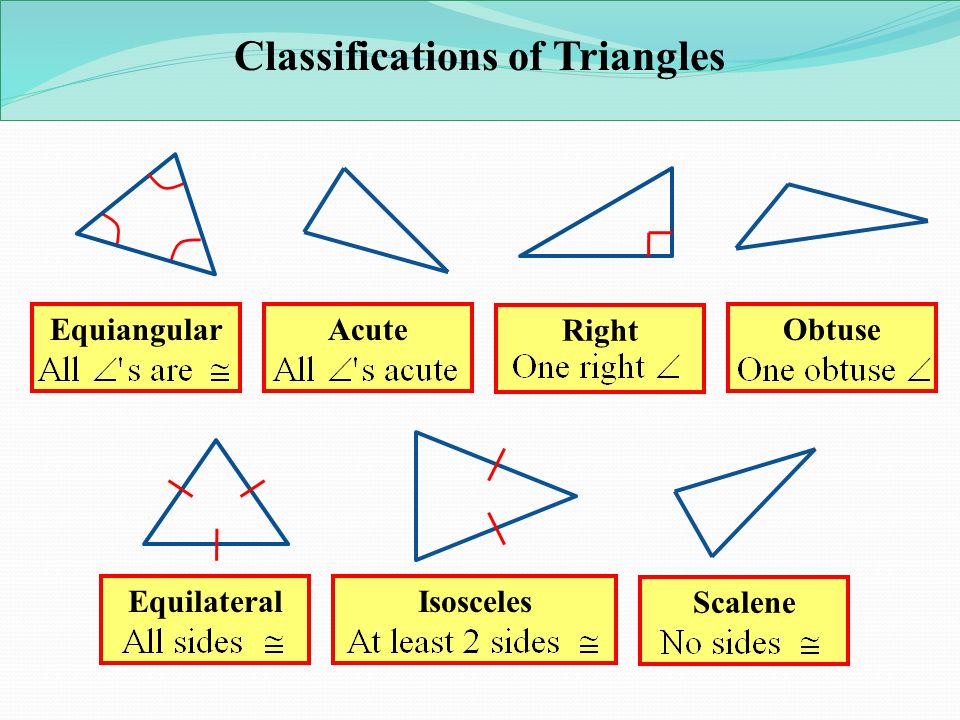
where, c is the length of the side opposite the right angle and a, b are the lengths of the other sides.
Right angle scalene triangles – Examples with answers
EXAMPLE 1
If a scalene triangle has a base of length 18 m and a height of 8 m, what is its area?
Solution: We use the area formula with the given information:
$latex A=\frac{1}{2}\times b \times h$
$latex A=\frac{1}{2}\times 18 \times 8$
$latex A=72$
The area is 72 m².
EXAMPLE 2
A scalene triangle has sides of lengths 12 m, 15 m, and 17 m. What is the perimeter?
Solution: We use the perimeter formula with the given information:
$latex p=a+b+c$
$latex p=12+15+17$
$latex p=44$
The perimeter is 44 m.
EXAMPLE 3
A right angle scalene triangle has sides of length 6 m and 8 m. What is the length of the third side given that it is the side opposite the right angle?
Solution: Here, we have to use the Pythagorean theorem.
What is the perimeter of a scalene triangle with sides of lengths 17m, 18m, 19m?
Choose an answer
$latex p=45$ m
$latex p=49$ m
$latex p=54$ m
$latex p=59$ m
What is the length of the side opposite the right angle if the other sides are 3m and 4m?
Choose an answer
$latex c=4.5$ m
$latex c=5$ m
$latex c=5.5$ m
$latex c=6$ m
See also
Interested in learning more about scalene triangles? Take a look at these pages:
- Area of a Scalene Triangle – Formulas and Examples
- Perimeter of a Scalene Triangle – Formulas and Examples
- What are the characteristics of scalene triangles?
- Obtuse Scalene Triangle – Formulas and Examples
- Acute Scalene Triangle – Formulas and Examples
Triangle | USE in Mathematics (profile)
A triangle is a figure that consists of three points that do not lie on one straight line, and three segments connecting these points in pairs.
In the figure:
$A,B,C$ are the vertices of the triangle.
$AB,BC$ and $AC$ are sides of a triangle.
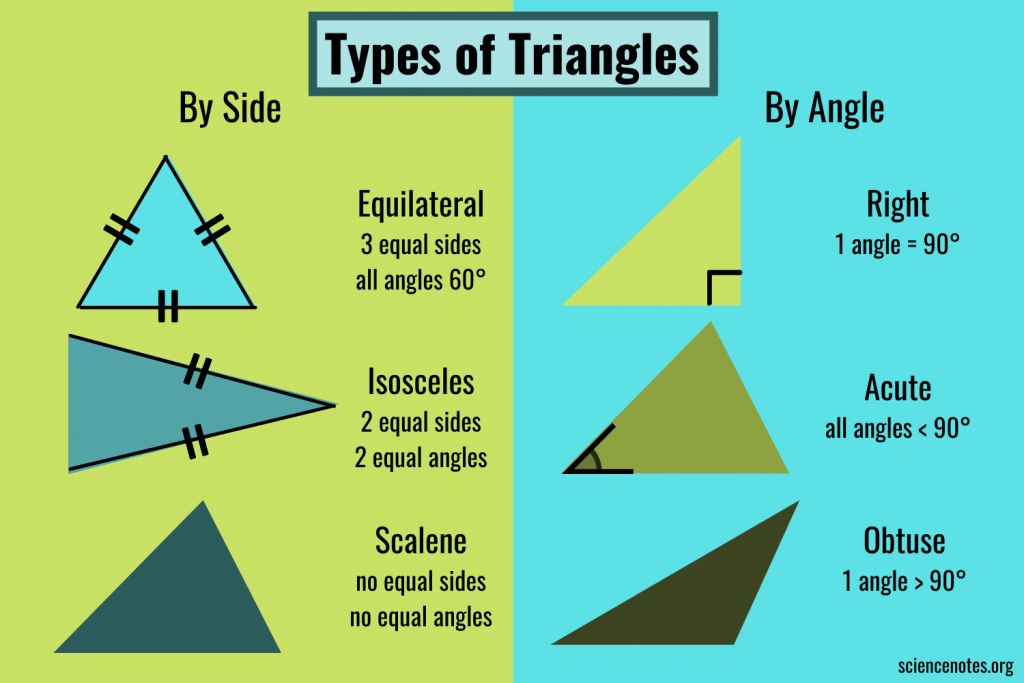
Types of triangles by angles:
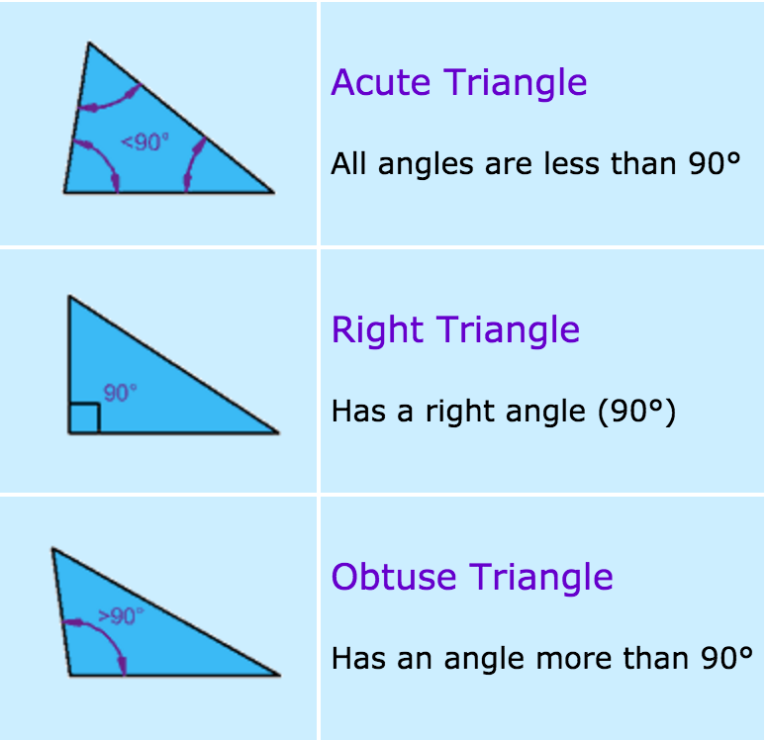
1. An acute triangle is a triangle in which all angles are less than $90°$, i.e. sharp.
2. A right triangle is a triangle with a right angle.
3. An obtuse triangle is a triangle containing an obtuse angle, i.e. angle from $90°$ to $180°$.
Types of triangles by aspect ratio:
1. An equilateral (regular) triangle is a triangle in which all sides and angles are equal.
2. An isosceles triangle is a triangle in which two sides are equal. Equal sides are called lateral. The third side is called the base.
3. A scalene triangle is a triangle in which the lengths of all sides are different.
Median, bisector, height
Median is a line segment that connects any vertex of a triangle with the midpoint of the opposite side.
The bisector of a triangle is the segment of the bisector of an angle of a triangle that connects a vertex to a point on the opposite side of the triangle.
The height of a triangle is the perpendicular dropped from any vertex to the opposite side (or its extension). This side is called the base of the triangle.
Basic properties of triangles:
- The sum of all angles in a triangle is $180°$.
- In an isosceles triangle, the angles at the base are equal.
- In an isosceles triangle, the height drawn to the base is both the median and the bisector.
- In an equilateral triangle, all angles are $60°$.
- An exterior angle of a triangle is equal to the sum of two angles not adjacent to it.
- The middle line of the triangle is parallel to the base and equal to half of it.
$MN$ is the middle line, since it connects the midpoints of adjacent sides.
$MN‖AC, MN={AC}/{2}$
Area of triangle: — the height drawn to the side $a$. 9{2}√3}/{4}$, where $a$ is the length of the side.
In a right triangle, legs are two sides of a triangle that form a right angle. The hypotenuse is the side opposite the right angle.
Some properties of a right triangle:
- The sum of acute angles in a right triangle is $90$ degrees.
- If one of the acute angles in a right triangle is equal to $45$ degrees, then this triangle is isosceles.
- The leg of a right triangle opposite the $30$ degree angle is equal to half of the hypotenuse. (This leg is called the small leg.)
- The leg of a right-angled triangle, which lies opposite the angle of $60$ degrees, is equal to the small leg of this triangle, multiplied by $√3$.
- The median of a right triangle drawn to its hypotenuse is equal to its half and the radius of the circumscribed circle $(R)$. (Fig.14)
- The median of a right triangle drawn to its hypotenuse divides the triangle into two isosceles triangles, the bases of which are the legs of this triangle. (Fig.14)
One acute angle of a right triangle is $44°$ greater than the other acute angle. Find the larger acute angle.
Solution:
In a right triangle $ABC$ $∠A$ and $∠B$ are acute.
Let $∠ A – x$, then $∠ B — (x+44)$.
The sum of acute angles in a right triangle is $90$ degrees.
Based on this rule, we will compose and solve the equation:
$x+x+44=90$
$2x+44=92$
The ratio between sides and angles in a right triangle:
In a right triangle $ABC$, with a right angle $C$
For an acute angle $B$: $AC$ — opposite leg; $ВС$ — adjacent leg.
For acute angle $A$: $BC$ — opposite leg; $AC$ — adjacent leg.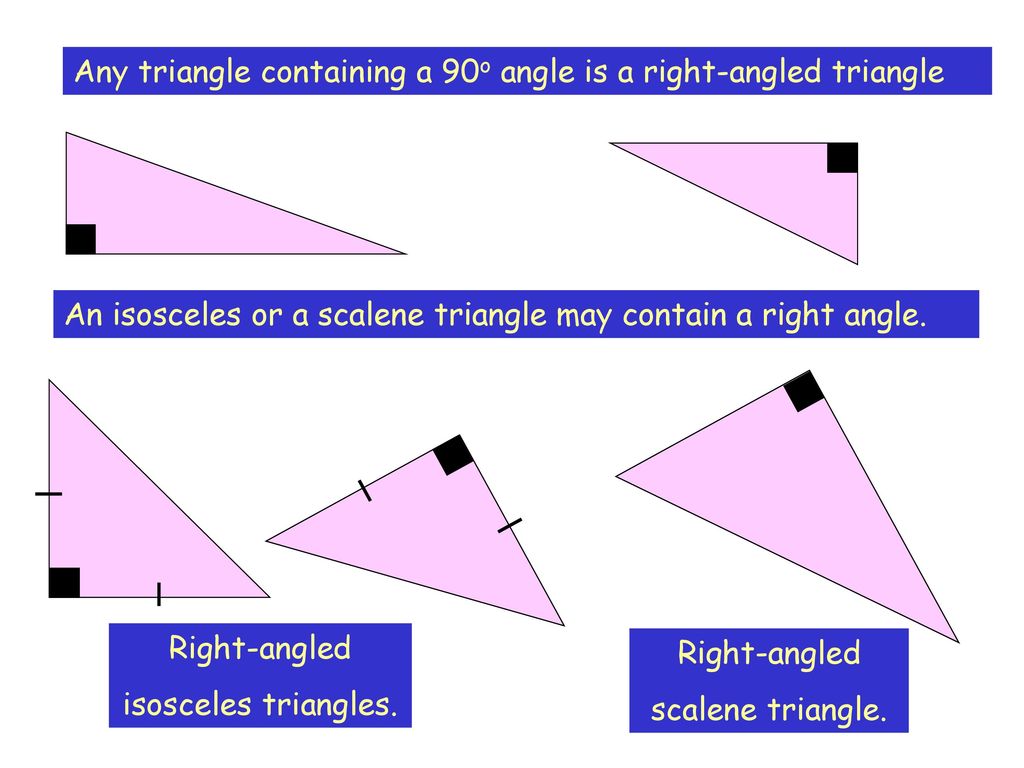
- The sine $(sin)$ of an acute angle of a right triangle is the ratio of the opposite leg to the hypotenuse.
- The cosine $(cos)$ of an acute angle of a right triangle is the ratio of the adjacent leg to the hypotenuse. 92x=1$
- In a right triangle, the sine of one acute angle is equal to the cosine of the other acute angle.
- Sines, cosines, tangents and cotangents of acute equal angles are equal.
- The sines of adjacent angles are equal, but the cosines, tangents and cotangents differ in signs: positive values for acute angles, negative values for obtuse angles.
Values of trigonometric functions of some angles:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctga$ | $√3$ | $1$ | ${√3}/{3}$ |
In triangle $ABC$ angle $C$ is a right angle, hypotenuse is equal to $39, cosB={5}/{13}$.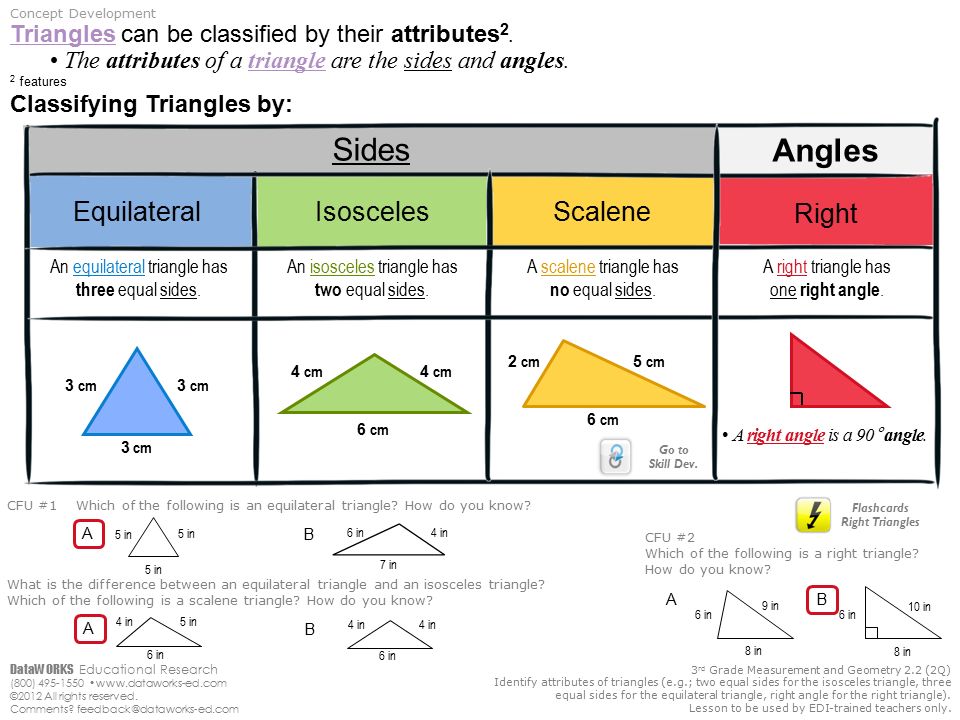
Find $AC$.
Solution:
Since we know the cos of the angle $B$, we write it by definition: the cosine of the acute angle of a right triangle is the ratio of the adjacent leg to the hypotenuse. In the triangle $ABC, AB$ is the hypotenuse, which is equal to $39$. $CB$ is the side adjacent to the corner $B$.
$cosB={CB}/{AB}={CB}/{39}={5}/{13}$
From the last two equalities, we obtain the proportion:
${CB}/{39}={5}/{13}$
$13∙CB=5∙39$
Divide both sides by $13$
$CB={5∙39}/{13}={5∙3}/{1}=15$
$AC$ find by the Pythagorean theorem.
In a right triangle, the sum of the squares of the legs is equal to the square of the hypotenuse.
92=(39-15)(39+15)=24∙54=1296$
$AC=36$
Answer: $36$
Practice: solve the 3rd task and training options for the exam in mathematics (profile)
Triangle. Definition formulas and properties of triangles.
In this article we will talk about the classification and properties of the main geometric figure — a triangle.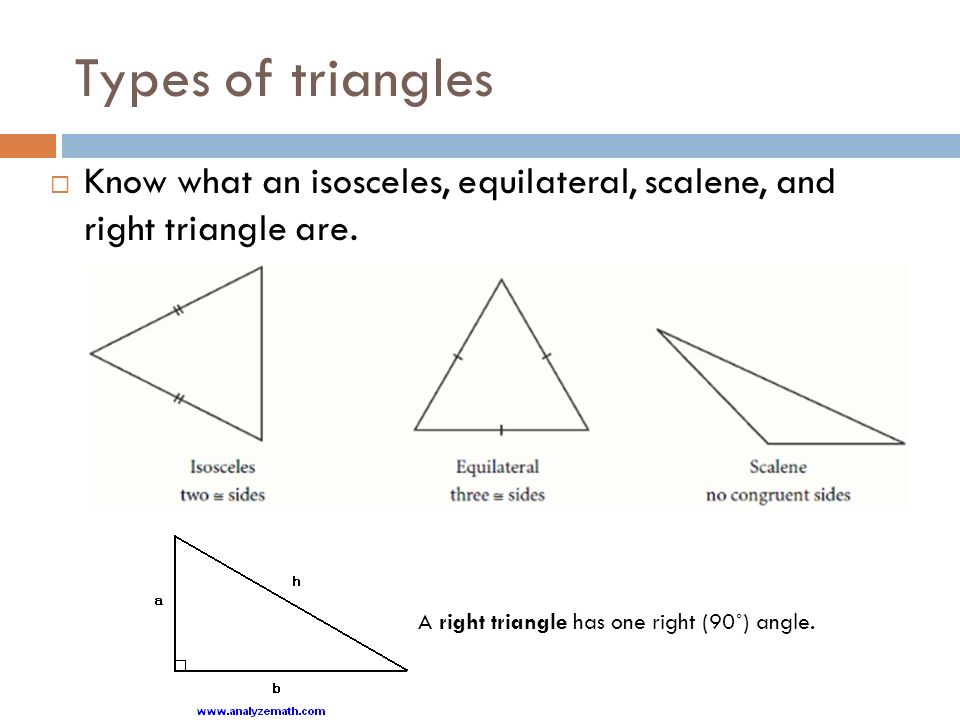
Contents:
- Triangle definition
- Classification of triangles
- Triangle Properties
- Triangle medians
- Triangle bisectors
- Triangle heights
Triangle definition
Triangle is a figure that consists of three points that do not lie on one straight line, and three segments connecting these points in pairs. The points are called the vertices of the triangle, and the segments are called its sides. In geometric problems, a triangle is usually depicted with a special symbol — △, after which the names of the vertices of the triangle are written, for example. △ABC.
Triangle ABC (△ABC)
- Points A, B and C are the vertices of the triangle. It is customary to write them in capital letters.
- Segments AB, BC and CA are sides of a triangle.
Usually the parties are assigned their names in small letters. The name is chosen from the first vertex of each side. Eg. side AB has the first vertex A, so this side is called a. That is, AB \u003d a , BC \u003d b , CA \u003d c .
- The sides of the triangle at the junction form three angles, which are usually named by the letters of the Greek alphabet α, β, γ. Moreover, opposite side a lies the angle α, b — β, c — γ.
The corners of a triangle can also be marked with a special symbol — ∠ . After which the vertices of the triangle are written in such an order that the vertex of the indicated angle is in the middle. For example:
- angle α — ∠BCA or ∠ACB;
- angle β — ∠BAC or ∠CAB;
- angle γ — ∠ABC or ∠CBA;
Classification of triangles
All triangles can be divided into several types, differing from each other in the size of the angles or the lengths of the sides.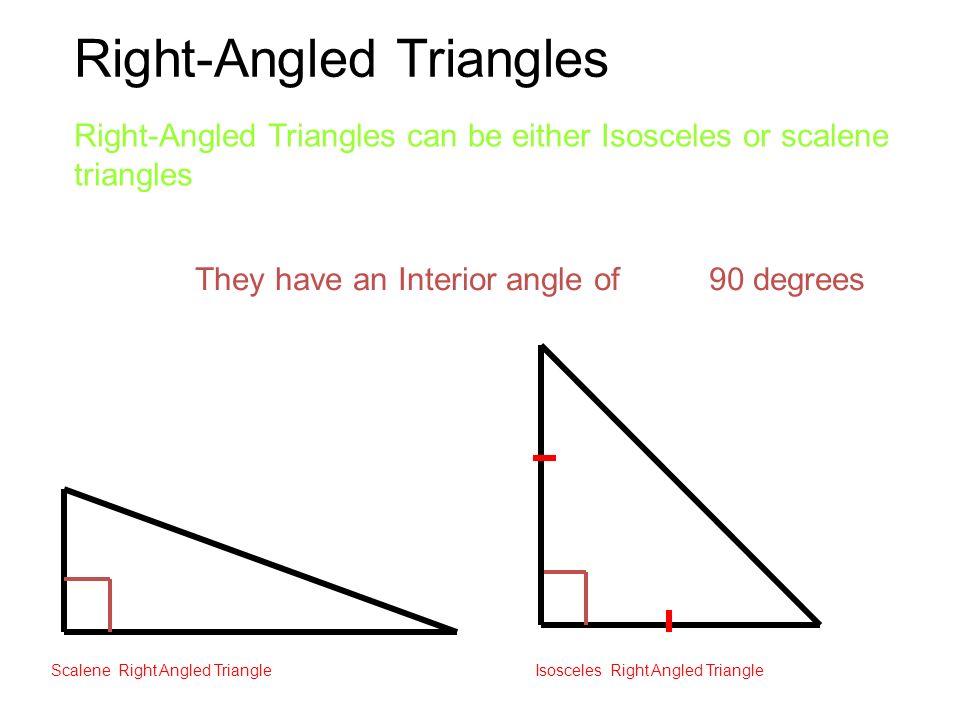
1.
Versatile is a triangle with all sides of different lengths.
a ≠ b ≠ c
∠ α ≠ ∠ β ≠ ∠ γ
2. Isosceles — a triangle in which the lengths of two sides are equal. They are called sides AB and BC. The third side is called the CA base. In this triangle, the base angles are ∠ α = ∠ β
a = b
∠ α=∠ β
3
. An equilateral (or regular) is a triangle in which all sides are of the same length. Also all its angles are 60°.
a = b = c
∠ α = ∠ β = ∠ γ = 60°
less than 90°
∠ α < 90°
∠β < 90°
∠ γ < 90°
5.
Obtuse is a triangle in which one of the angles is greater than 90°. The other two angles are acute.
∠ α < 90°
∠β < 90°
∠ γ > 90°
6.
∠ α < 90°
∠β < 90°
∠ γ = 90°
Triangle Properties
1. Properties of angles and sides of a triangle.
- The sum of all angles of a triangle is 180°:
α + β + γ = 180°
- The sum of the lengths of any two sides of a triangle is greater than the length of the remaining side:
a + b > c
b + c > a
c + a > b
- In a triangle, a larger angle lies opposite the larger side, and vice versa. Equal angles lie against equal sides:
if α > β then a > b
if α = β, then a = b
2. Sine theorem.
The sides of a triangle are proportional to the sines of the opposite angles.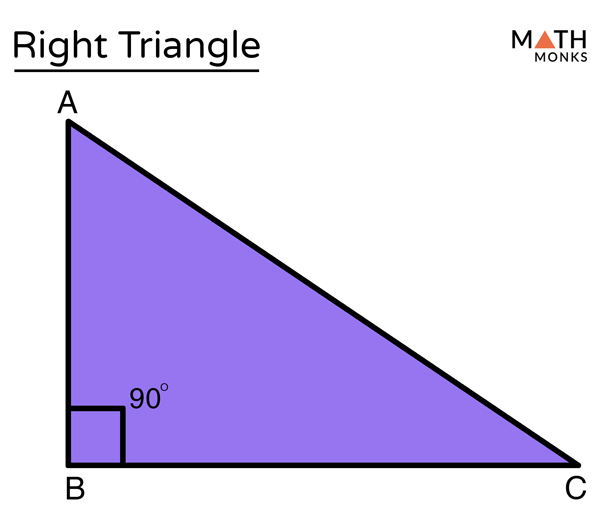
| a | = | b | = | c | |
| sin α | sin β | sin γ |
3. Cosine theorem.
The square of any side of a triangle is equal to the sum of the squares of the other two sides of the triangle minus twice the product of those sides times the cosine of the angle between them.
a 2 = b 2 + c 2 — 2bc cos α
b 2 = a 2 + c 2 — 2ac cos β
c 2 = a 2 + b 2 — 2ab cos γ
b = a cos γ + c cos α
c = a cos β + b cos α
Triangle medians
Triangle median is a segment inside a triangle that connects the vertex of the triangle with the midpoint of the opposite side.
Triangle median properties:
1.
1)
| A.O. | = | BO | = | CO | = | 2 | |
| OD | OE | OF | 1 |
3. The median of a triangle divides the triangle into two parts of equal area
S ∆BEA = S ∆BEC
S ∆CBF \u003d S ∆CAF
4. The triangle is divided by three medians into six equal triangles.
S ∆AOF = S ∆AOE = S ∆BOF =
= S ∆BOD = S ∆COD = S ∆COE
5. The vectors that form the medians can form a triangle.
Triangle median formulas
Triangle median formulas in terms of sides:
m
m b = 12√2a 2 +2c 2 -b 2
m C = 12√2a 2 +2B 2 -C 2
Formulas of the parties through medians
A =
√2 (M b 2 +M 2 )-m a 2
b =
√2(m b 2 +m c 2 )-m b 2
c =
√2(m b 2 +m c 2 )
Triangle bisectors
Angle bisector of a triangle — a ray with the beginning at the vertex of the angle, dividing the angle into two equal angles.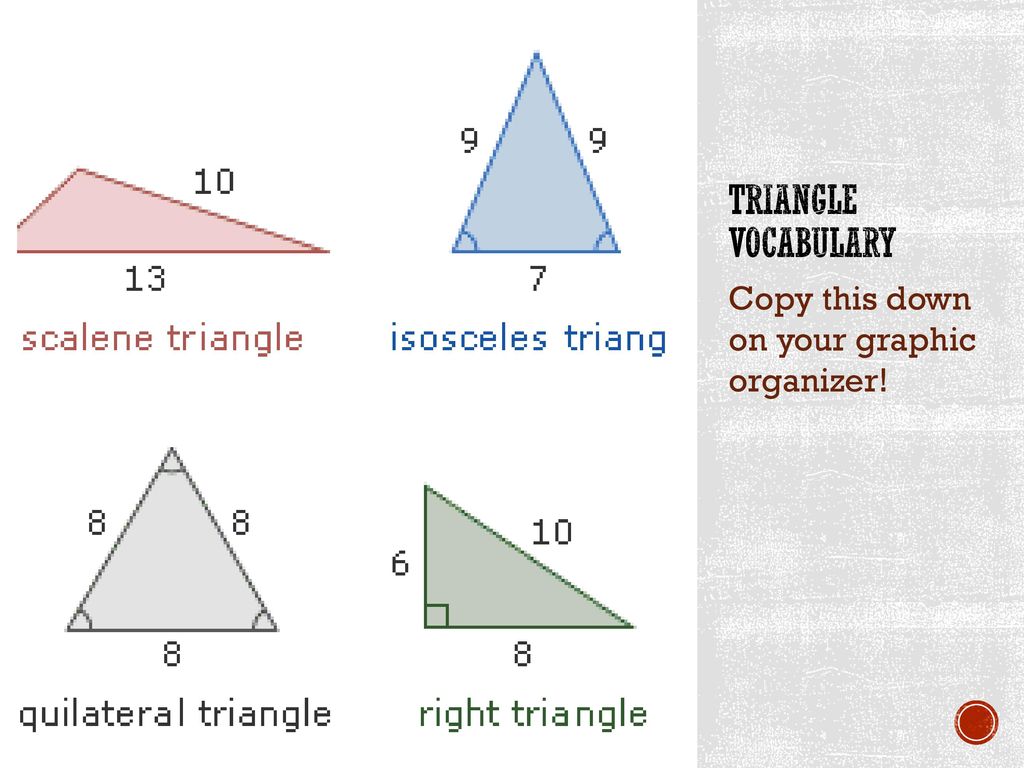
Triangle bisector properties:
1. Triangle bisectors intersect at one point O , which is called INCENTER. The incenter is equidistant from the three sides of the triangle, therefore the incenter — the center of the inscribed circle .
2. The bisector of a triangle divides the opposite side into segments proportional to the adjacent sides of the triangle .
| AE | = | EC |
| AB | B.C. |
3. The angle between the bisectors of the inner and outer corners of a triangle at one vertex is 90°.
Angle between La and La’ = 90°
4. If two bisectors in a triangle are equal, then the triangle is isosceles.
5. If three bisectors of a triangle are equal, then the triangle is equilateral.
Formulas for the bisectors of a triangle
Formulas for the bisectors of a triangle in terms of the sides:
Lb =
√bcp(p-b)
a+c
Lc =
√bcp(p-c)
a+b
p =
a + b + c
2
Triangle bisector formulas in terms of two sides and an angle:
La =
2bc cos
a+b
Lb =
2ac cos
a+c
Lc =
2ab cos
b+c
Triangle heights
The height of a triangle is the perpendicular dropped from the vertex of the triangle to the opposite side.

 This relationship is known as the Pythagoras theorem.
This relationship is known as the Pythagoras theorem.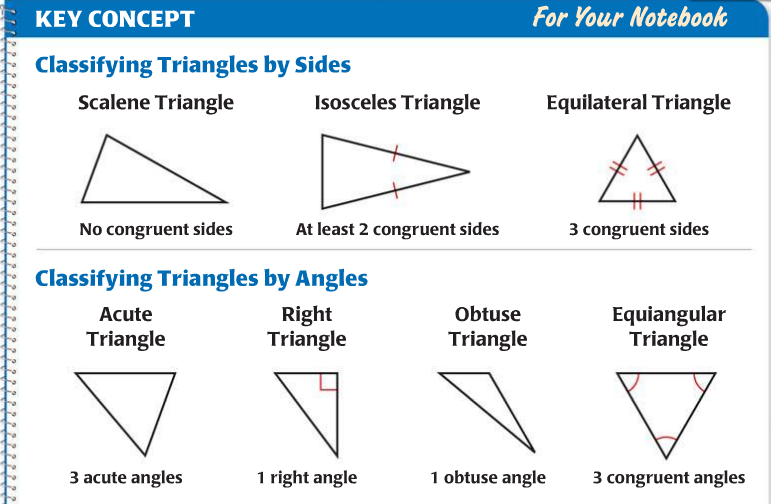 Here, the given three side lengths are 5 units, 12 units, and 13 units. So, the perimeter = 5 + 12 + 13 units, which is 30 units. Therefore, the perimeter of the given scalene right triangle is 30 units.
Here, the given three side lengths are 5 units, 12 units, and 13 units. So, the perimeter = 5 + 12 + 13 units, which is 30 units. Therefore, the perimeter of the given scalene right triangle is 30 units.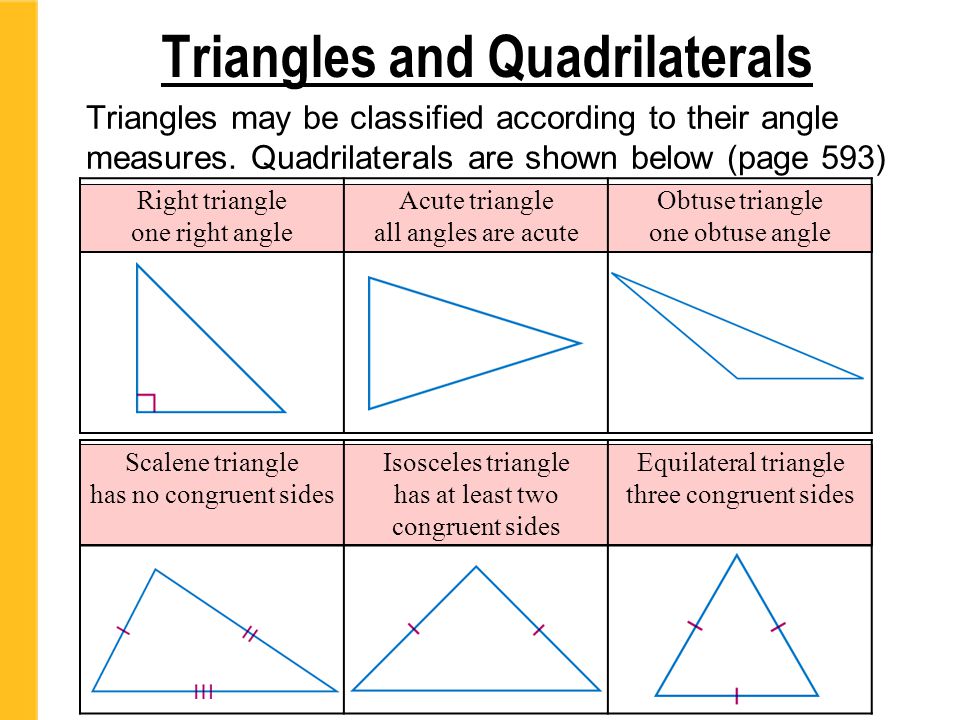
 Usually the parties are assigned their names in small letters. The name is chosen from the first vertex of each side. Eg. side AB has the first vertex A, so this side is called a. That is, AB \u003d a , BC \u003d b , CA \u003d c .
Usually the parties are assigned their names in small letters. The name is chosen from the first vertex of each side. Eg. side AB has the first vertex A, so this side is called a. That is, AB \u003d a , BC \u003d b , CA \u003d c .